In 1889, Irish engineer Robert Manning produced an equation for calculating flow in open conduits from the level in the channel.
Manning's equation:
V = Rh2/3 • S1/2
Q = VA, where
Q = Volumetric flow
A is the cross-sectional area of the wetted perimeter,
V is the cross-sectional average velocity,
k is the units conversion factor,
n is the coefficient of friction,
Rh is the hydraulic radius,
S is the slope of the channel.
Although tables of Manning's "n" are common, it is nearly impossible to accurately calculate "n," so it is almost always an educated guess, based on the engineer's experience and expertise. A small change in "n" can result in a large change in "V" and thus a large change in "Q."
For real accuracy, the use of a primary device is required. These are restrictive devices placed in the flow stream that raise the height of the water behind the restriction to a predictable level based on volumetric flow. Typically, these are flumes and weirs.
Flumes and Weirs
Early in the last century, hydraulic engineers discovered that there was a relationship between the head height behind a constriction in the channel and the flow rate through the constriction. This relationship takes the form of:
Q = KHn
where Q is volumetric flow, K is a units constant, H is the head height, and n is a coefficient that is related to the size and type of constriction.
These constrictions can be divided into two basic groups, flumes and weirs. There are various types of each.
Figure 2. Measurement weirs come in several configurations: v-notch, rectangular and trapezoidal, among others.
Courtesy of Water Measurement Manual, 3rd ed., U.S. Dept. of the Interior, Bureau of Reclamation
In a v-notch weir, all the water flows through the weir, and the level is measured at a known point behind (upstream) of the weir. This level forms the "H" in our formula.
Sometimes, if very high accuracy is required at the lowest flow rates, a compound weir can be used. This is often a rectangular weir with a sharp v-notch forming the bottom of the weir. Thus, the rectangular weir equation can be used for high flows, and once the flow reduces to below the zero point of the rectangular weir, the v-notch equation is used. Many open channel flowmeters have the ability to switch equations like this.
Flumes have a constriction in the flow, and a "hydraulic jump" that causes the head height to be linear and repeatable. There are dozens of kinds of flumes. In modern times, the most common are the Parshall and the Palmer-Bowlus flumes.
Figure 3. Parshall Flumes measure flow at the inlet and outlet of wastewater treatment plants and intakes at power plants.
Courtesy of Water Measurement Manual, 3rd ed., U.S. Dept. of the Interior, Bureau of Reclamation
Making Flumes and Weirs Work
For a flume or weir to be accurate, it must be installed properly. Most error problems with open channel flow measurements are traceable to the accuracy of the flume or weir, not the level measurement or the flow transmitter.
All flumes and weirs must be installed as close to perfectly level inlet-to-outlet as possible, and side-to-side, too. Fiberglass flumes often "bow in" when concrete is poured behind them, and this produces unexpected inaccuracies, which may not be able to be calibrated out, except by in-situ flow testing and the use of a strapping table in the flowmeter.
All flumes and weirs have what is called the "submergence point" where the level goes above the measurement range of the device. Flow may continue to be moving in either direction during submergence, but the measurement is meaningless during that condition.
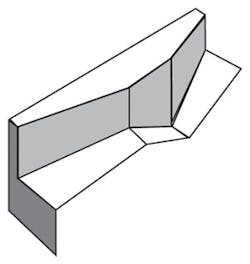
A Palmer-bowlus flume
Figure 4. Palmer-Bowlus flumes measure flow in
sewers and other open conduits where there is
relatively low flow.
Courtesy of Water Measurement Manual, 3rd ed.,
U.S. Dept. of the Interior, Bureau of Reclamation
The Datagator
Figure 5. The Datagator can measure above the
submergence point of the standard flume and in both
forward and reverse directions.
Courtesy of Renaissance Instruments
In the early 1990s, a special kind of flume was invented, tradenamed Datagator. This primary device is based on a Palmer-Bowlus flume, but is capable of measuring above the submergence point of the standard flume, as well as measuring flow in both forward and reverse directions (Figure 5).
Level Measurement Instrumentation
There are many ways to measure the level behind a flume or weir. The oldest, based on the Nilometer, is the Mark I Calibrated Eyeball with a staff gauge. A staff gauge is a ruler-like device mounted at the measurement point in the flume, weir or channel. The user "eyeballs" the reading on the staff gauge and
records the level for use in calculating volumetric flow.
Other types of level measurement devices that have been used for open channel flow monitoring include ultrasonic (downlooking) and ultrasonic (uplooking); pulse radar, differential pressure transmitters, and capacitance and RF admittance devices.
For many years, floats have been used, with stilling wells, to measure the level in the channel or flume or weir. Each of these types of level measurement devices have their features and benefits, but the accuracy of each as a flow measurement instrument is dependent on the accuracy and correct installation of the flume or weir of which it is measuring the level.
So now you have a quick, back-to-basics look at open channel flow monitoring.
Flow Like An Egyptian: The Basics of Open Channel FlowI'm Walt Boyes, and if you are like most automation professionals, you don't do flow measurement design daily or even weekly. So some of the basics may be new to you…especially in the area of open channel flow. Here is a PDF presentation to help you understand more the basics of open channel flow. |
Latest from Flow

Leaders relevant to this article: