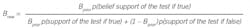Belief is the confidence that you have in making a statement of fact about a supposition. Here are some examples of statements we might make:
- “These symptoms are just seasonal allergies.”
- “The average benefit of Treatment Y is greater than that of Treatment X.”
- “The process has reached steady state.”
And for each we might claim to be very certain of the supposition (perhaps 99% sure), or somewhat certain (perhaps 80% sure), or even not sure whether it is or is not (perhaps 50% sure).
Bayes Belief, B, is scaled by 100%, so the value is 0 ≤ B ≤ 1. If you tend to question a statement, the belief that it's true, B, might be 0.25. If you are fairly certain, B might be 0.97. If you're not so sure about something and it could be a 50/50 call, then B = 0.5.
Because we take action on suppositions, we want to be fairly certain that the statement about what we suppose represents the truth about the reality. When you're not certain, you perform tests, take samples, get other opinions, etc. to strengthen or reject your belief in the supposition. But tests aren't perfect. There's always some uncertainty about the results.
A test for steady state (SS) might look at the past several data points. At SS, the time-rate of change, or data slope, ideally is zero, S = 0. But, because of noise on the data, the slope will not be exactly zero; so, you might accept SS if the test results are -0.1 ≤ S ≤ +0.1. If the measurements indicate S = -0.03 you say that is just noise, and the test indicates SS. But, at SS, a particular confluence of data perturbations might indicate the local slope is S = 0.15, and the test would reject the true condition of SS. Maybe, given a true SS, the test will indicate SS 85% of the time, and reject SS 15% of the time.
On the other hand, if the process is in a transient state (TS), the slope will be much greater than a SS value, and the slope will be beyond the -0.1 ≤ S ≤ +0.1 limits, and the test result will claim TS. However, even in a transient, when the process variable is moderately changing, the noise pattern on the past few samples might have a counter trend, and the rate of change might incorrectly indicate SS. Maybe, given a true TS, the test will indicate TS 95% of the time and SS 5%. A matrix of the probabilities of the test giving true and false indications is shown in Table I.
Table 1: Probabilities of correct identifications and false positives and negatives for a process test.
If you somewhat believe something is possibly true, B = 0.75, and you do a test that supports your belief (indicates it's probably true), then your belief value rises, perhaps it becomes B = 0.99, which may be strong enough belief to take action on it. But, if the test indicates it's probably not true, your belief decreases. Maybe it falls to 20%, somewhere between zero and your former belief of 70%. If a second test also indicates the hypothesized benefit is probably not true, your belief declines again, perhaps to 1%, which may be enough to reject the supposition.
There are two different aspects to knowledge in this analysis. Keep them separate. First, there's the truth about the situation. The patient either has the disease or does not. The process is either at SS or not. Treatment Y is either better than Treatment X or not. The truth is stated in the left-most column of the tables. However, the truth isn't known, so we use a test.
The second knowledge aspect is the test result. The test either indicates positive or negative results, or that Y is better than X or it is not. The test outcome is stated in the top row of the tables. But the test is not infallible. The test results may, or may not, represent the truth.
Also, there are two different aspects to probabilities in this analysis. Keep them separate. The first is the entries in the table, the probability of a test giving a correct or wrong outcome.
The second probability aspect is the belief, the personal confidence that something is true. But just because the person wants to believe it is true (or not true) does not make it so. (Humans used to believe that the sun revolved around the Earth, but the belief did not make it so.)
Belief changes with successive test results. The Bayes Belief method for updating belief after test results is:
where Bprior is the belief prior to the test results, and Bafter is the belief after the results. The numerator is the expected outcome if the supposition is true. The denominator is the sum of all such test outcomes that are possible (whether the supposition is true or not true).
The belief could be in either of the two mutually exclusive cases. For example, that Y is better than X, or that X is better than Y. Or that the patient has cancer, or does not have cancer. It doesn't matter which supposition you choose.
The test results could either support or counter the belief. The term p(belief support of the test) is the probability from Table 2.
Table 2: Generic probabilities of correct identifications and false positives and negatives.
The probabilities in the four categories often can be determined from controlled testing on known situations. But, just as often, they can be reasonably estimated from experience. In either case, don't think the probabilities are perfectly known. They have error. But in my experience, the uncertainty on the reasonable values doesn't undermine this method for propagation of Belief. Alternate p-values might lead to needing one more or one fewer tests to provide adequate confidence to take action.
After each trial, you'll know more about your process and the probabilities. So update probabilities using your developing knowledge.
What is adequate confidence to take action? If B = 0.99 then you're very certain the supposition is true. If B = 0.01 then you're equivalently confident that it's untrue. But to take action, be sure that the consequences of a wrong decision, tempered by the probability of a wrong decision, are acceptable. Risk is the probability of an event (you can substitute Belief) times the undesirable consequences. Benefit is the Belief in an event times the desirable outcome. Set the threshold of Belief to take action by the consequences of taking a right or wrong action (accepting A when it should be B; taking B when it should be A, etc.).
Many accept this as a very good guide to updating belief with sequential results, and then using the belief to make decisions. Alternately, although purists accept the mathematical model, many of them object to the method because of the uncertainty on the values for either probabilities, or the initial belief, or the threshold to take action.
Of course, humans might not want to follow this kind of logical rule. Often, when they know something is true, they consider themselves to be absolutely sure, and rather than admit they were wrong, they reject any data that would counter their personal belief. Or when they want something to be true, they reject any opposing data. Here are some examples I’ve encountered:
• “Our sports fans are kind and gracious, but our opponent’s fans are disrespectful, poor sports.”
• “My kid is the best looking, smartest and most athletic in the entire class.”
• “Reel mowers are better than rotary mowers.”
If your boss or significant other knows the truth, or wants a particular outcome, and the resulting action from an erroneous belief has less adverse consequences than the personal cost and effort of proving that person wrong, it might be best to let it go their way. Only martyrs let logic lead to a confrontation against authority. On the other hand, I would hope that each of us protect ourselves, our organizations and society from action based on erroneous beliefs.
This is an approach to use fallible data to logically temper or support a fallible human belief. Practice applying this propagation of belief in your personal and professional life. Understand the concept, then you'll be able to qualitatively (subjectively, intuitively) apply it. You don't need perfect probabilities in the table. Develop your potential, then promote this approach to others in charge.
