Control Valve Simulation
Ask the Experts is moderated by Béla Lipták, editor of the Instrument Engineers Handbook . In this column, he and other experienced process control engineers welcome questions concerning process measurement and control and optimization. If you are qualified and would like to be on our expert team, please send us your resume. Process control-related questions should be accompanied by P&ID sketches using ISA symbols.
Q: Im developing an automation and control project for a water treatment process. I would like simulate the designs before putting them into operation. For that reason, I need a model for simulating control valves (proportional). It doesnt need to be a high-level simulation. I only need to build a kind of block with two inputs and two outputs (a MIMO system). Those inputs are the incoming water flow and the signal from the controller (0%-100%). The outputs are the outgoing water flow and the valve position (0%-100%). It sounds simple, but doing it using Simulink (from Matlab) could be complex. At the university, I used to go for Simulink in order to get simulations for controlling electronic systems, but I have never carried out sims for hydraulic models. (I also need the fuzzy blocks of Simulink). I know of software like Hysys or Fluidsim... but I dont need such a level of reality in my simulations and I haven´t got the money to buy them.
Valve Configuration Parameter
I already had read your article, How to Select Control Valves, Parts 1, 2, 3 and I could finally understand many concepts relative to control valves. I would like that you advise me about how to build this simulation block in the simplest way so that four signals can interact between them?
From your article I understand that Gv is a constant, Gv = [Δflow/Δ%], but I couldnt understand how to operate the input signals inside the block!
How do you mathematically modify the admission flow area inside the valve body according to the signal from controller without multiplying the incoming flow signal and convert the valve in a kind of signal flow amplifier?
Christian Casas Buitrago
Occidental de Colombia, Inc.
[email protected]
A: As I understand it, you want to get a general approximation of a control valve operating in a flow loop, but you do not need the precision and detailed accuracy required by simulation programs such as Simulink, Hysis or Fluidsim, nor do you wish to incur the costs of those rather expensive programs.
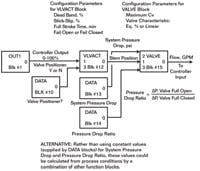
PC-ControLAB 3, a process control loop training and simulation program, is intended primarily for use in training seminars. It permits users to practice controller tuning and to view the behavior of various types of control loops, including feedback, feed-forward, ratio, cascade, override and decoupling. Of immediate interest to you, however, is the process model building program that comes with PC-ControLAB. Using a function-block oriented program it is extremely simple to graphically configure a process model that resembles a real process.
The control valve is configured by two function blocks: One block simulates the valve actuator, and another block simulates the hydraulic characteristics of the valve body itself. The first function block permits setting characteristics of the actuatordead band, stick-slip and whether or not it has a positioner. The second function block permits setting features of the valve itself, such as maximum Cv, equal percent or linear valve. External inputs to this block permit setting the system pressure drop and pressure drop ratio.
PC-ControLAB 3 sells for $495 for a single-user license, and is available either through Wade Associates, Inc. or through ISA. You can download a demonstration version of the program from www.wadeco.com.
Because of the many features of this program, I think you would find it useful to your career in many areas beyond your immediate problem. If you have additional questions, please contact me.
Harold Wade
Wade Associates, Inc.
[email protected]
A: I have great appreciation for simulating a process to gain understanding of the process control dynamics. The problem is always to develop a model which is as close to reality as is needed. A simple static model can provide information for a steady-state system, but is of little value for discovering dynamic response and predicting control issues.
Valve flow = (Co, Positioner dynamics, pressure difference, valve characteristic, piping and pump characteristics, fluid density, (and sometimes Reynolds Number), valve dynamic response and response to step inputs. Co = controller output signal. See The Instrument Engineers Handbook for these topics and references to the applicable standards.
In modeling dynamic systems I have sometimes found it valuable to cycle through the calculations a number of times until the numbers settle out and converge before moving to the next step in time. The time constants in process control systems often differ greatly in size and make a stiff system. The computer does not mind the extra arithmetic. Dont forget any significant time lost in the control system.
Here are a few comments on a favorite topic.
The first thing is to define the purpose of the model. A simple model will give simplistic information. I have used this for preliminary sizing and estimates. W = 63.2*Cv√(∆P)∕(density). W = pph, and 63.2 is a constant for the units used. Cv is the flow coefficient for the valve at the specific percentage open. ∆P is pressure difference in psi. Density is in pounds/cu ft.
In real life, Cv is a non-linear function of the valve stem position. This is found in the catalogs. Valve stem position is a function of controller signal and positioner accuracy. A complete model will include the estimated slip-stick motion of the valve stem. A more complete model will consider the possibility of choked flow or cavitation. If the flow fluid is compressible the appropriate equations consider those effects.
The standard definitions and equations are in the references below. Note that, in general, these equations are more reliable over reasonable ranges. Flow coefficients and even flow regimes can change widely at small valve openings. There is still debate over flow at low Reynolds numbers. Fluids at high viscosities are troublesome.
ANSI/ISA-75.01.01-2002 (60534-2-1 Mod), Flow Equations for Sizing Control Valves.
ISA-75.25.01-2000 (R2006), Formerly ANSI/ISA-75.25.01-2000, Test Procedure for Control Valve Response Measurement from Step Inputs
Cullen Langford, PE
A: There are two considerations in simulating valves: steady-state and dynamic. The steady-state model converts valve position into flow through the valve characteristic and pressure drop. The dynamic model converts controller output into valve position through deadband and velocity limit or the possible presence of a positioner, which closes the loop around the valve position through proportional or PID control.
Valve behavior is not a trivial consideration in fast loops like flow and pressure. Dead band can cause endless limit-cycling in level loops, and velocity limit can create expanding cycles on a large upset.
Simulation of all these properties is described in my book, Simulating Process Control Loops, ISA, 1990, pp. 125-131. Unfortunately, it is now out of print, but might be found in an engineering library.
Greg Shinskey
Process Control Consultant
Q: My name is Matt Wilhite, Advanced Development Manager at Molex.
One of my colleagues has written a PhD thesis on the use of process control in electroplating. He and his sponsoring university (University of Limerick) are seeking a qualified external examiner to examine his thesis. Hopefully someone would see this as a potential opportunity to work with us in future or gain from our experience somehow. All travel and accommodation expenses for you or designate would be 100% paid.
I can be contacted by email and phone (mobile is easiest) listed below at any time.
Matt Wilhite
Molex Ireland Ltd.
Shannon Industrial Estate
Shannon, Co. Clare, Ireland
[email protected]
int + 353 (0)61 702420 (office)
int + 353 (0)86 8157115 (mobile)