This column is moderated by Béla Lipták, automation and safety consultant and editor of the Instrument and Automation Engineers' Handbook (IAEH). If you have an automation-related question for this column, write to [email protected].
My question concerns a custody-transfer metering skid using 30-in. ultrasonic flowmeters, which are claimed by the supplier to have 0.01% of actual reading accuracy, 0.05% repeatablility and 20:1 rangeability covering velocity ranges from 5 fps to 100 fps. They are four-path-design Emerson Daniel SeniorSonic 3414, which can be found on at www.emerson.com/en-us/catalog/daniel-3414.
My question is: Does your handbook suggest that the measurement error would be cut in half if we had four sensors and averaged their outputs?
M. Taghvar
[email protected]
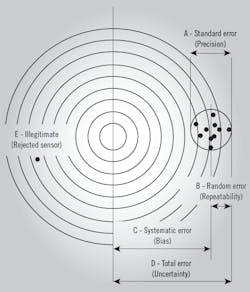
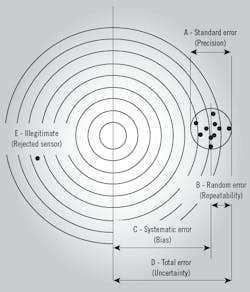
A: The accuracy-related terms are shown in Figure 1, using the example of target shooting. The diameter of the spread of the 10 penetrations in the right (A) is called precision or standard error. The radius of that spread-circle (B) is called repeatability or random error. The distance between the center of the target (which is the calibration reference point) and the center of the spread circle (C) is called bias or systematic error, and the distance between the calibration reference and the furthest penetration (D) is called total error or total uncertainty. Most users think of D as the accuracy of the measurent, but the specifications of the vendors often do not clearly state what they call accuracy.
Figure 1: In this "shooting target" representation, the diameter of the spread of the 10 penetrations in the right (A) is called precision or standard error. The radius of that (B) is called repeatability or random error. The distance between the center of the target (which is the calibration reference point) and the center of the spread circle (C) is called bias or systematic error, and the distance between the calibration reference and the furthest penetration (D) is called total error or total uncertainty.
In your case, the vendor's specification is wrong, because the total error D (accuracy) can not be smaller than the repeatability (B). It can’t even equal it, because the only way for D to equal B is if C = 0, and even that would assume perfect calibration, which doesn’t exist. So the claim that the total accuracy of this flowmeter is 0.01% when its repeatability is 0.05% is impossible. The rangeability claim of 20:1 (5-100 fps) is possible, but the accuacy in terms of % actual reading (%AR) will not be the same throughout the range—it will be better at high speeds than at low ones.
The supplier does not state if this sensor was calibrated and if it was, against what reference. The probability is that this is a "partially calibrated" meter, meaning that the meter is uncalibrated and only the electronics are tested against a simulated signal.
As to your question concerning error reduction by using multiple meters, the statement in my book is correct, but only in the theoretical case when C = 0, which assumes perfect calibration. Also, the error will not be reduced by increasing the number of sensors if the measurements are not independent, but have a common bias (systematic error) due to having common calibration or installation errors.
In short, the capabilities of your sensor are overstated and putting in more of them will not reduce the measurement error.
Béla Lipták
[email protected]
A: There are two common classifications of measurement error. One is accuracy (also called bias, or systematic error) and the other is precision (also named random error). Calibration adjusts the measured value to make it as close to the true value as possible. Precision is not improved by calibration, accuracy is.
You mention, “Some reports suggest that measurement error in that case will be reduced by the square root of the number of sensors in parallel.” This is a classic statistics central limit theorem conclusion, or propagation of uncertainty conclusion. It means that averaging multiple measurements can reduce the variation associated with an individual measurement. If the measurements are accurate, if there is no systematic error, but just random error, then averaging multiple measurements will improve the closeness of the composite measurement to the true value. It will improve accuracy. For your question, assuming calibration is perfect for each of the four sensors, and that each of the four measurement errors are independent, then yes, the closeness of the average to the true value will be about half that of any individual measurement.
However, it does require that the samples each represent independent measurements and that they have no common bias. For example, if the sensors are all installed identically, but improperly, or if they are all calibrated with a common error, then the measurement error (the bias of the average, the systematic error, the accuracy of the average) will not be reduced by increasing the number of sensors.
Replicate sensors and voting (reporting a middle-of-three values) is common when sensors are subject to frequent failure, but if the objective is to improve either accuracy or precision, then installing better sensors or improving calibration procedures will be more economically beneficial than installing (and independently maintaining and calibrating) multiple sensors.
Both supplier and customer have economic risk associated with material meters, and both desire that the measurement methodology represents best practice on a cost-to-benefit basis. But, the customer is probably as interested in BTU content of the gas, which changes with composition. So, be sure to address the true economic value of the gas, not just the volume metered.
R. Russell Rhinehart, emeritus professor
[email protected], www.r3eda.com
Q: What is the ideal college degree for process control? Sometimes, I see people with chemical engineering degrees and sometimes they have electrical engineering degrees. Which is ideal? Or is there a process control degree available, and if so, where? What is the ideal degree?
Mohammed AbdulRasool
[email protected]
A: Your question brings up the topic of recognition of our profession by the educational institutions in general. For example, I have ME degrees, I was teaching automation and process control in the ChE department of Yale University, and my handbook is published by the EE deparrtment of my publisher. Was this my choice? No, the reason was that there was no such department as Automation and Process Control (A&Pc) at these institutions. Was that because they didn’t consider our profession worthy of a separate department? No, they didn’t offer an A&Pc degree because they didn’t even know that our profession exists.
This is a strange situation, because to control a process, we not only need the knowledge of all fields of engineering, but more. We need to understand how processes react to inputs. We have to understand their "personality" when uncontrolled and their behavior when controlled. We have to know how to obtain the information needed to know all that, how to bring that information to our control algorithms, and from there to the manipulated variables. And how to protect our systems from hacking, and how to do that safely in the analog, digital or wireless environments. Well, to even start to learn all of that takes four years, so it deserves a separate department and a separate A&Pc degree.
Right now, I am writing a book showing how the knowledge gained by the A&Pc profession can be applied to non-industrial processes, why the behavior of all processes (industrial or not), can be analyzed by our methods, and how this analysis can help to close the debate and quantify the consequences if certain non-industrial, long-deadtime, high-inertia, integrating processes (such as global warming and artificial intelligence) are left uncontrolled, how to bring them under control, and how much time is available to do that.
Béla Lipták
A: University of Alberta has an undergraduate degree in Process Control, and has had it for more than 30 years. Canada also offers a recognized trade for instrumentation available from a number of colleges.
Ian Verhappen
[email protected]
A: My understanding is that our Process Dynamics and Control course underwent a major restructuring in the 1990s to include, among others, an experimental component. In addition, the covered material was modified to include more advanced concepts, based on the textbook „Process Dynamics, Modeling, and Control” by Professors Ray and Ogunnaike (former student of Prof Ray) (www.amazon.com/Process-Dynamics-Modeling-Babatunde-Ogunnaike/dp/0195091191)
Since then, additional changes have been made to include, for example, "virtual" experiments. In parallel with these efforts, the department has recognized the importance of statistics in industrial practice, so Professor Zavala is currently developing a senior/graduate-level course on statistics and, more broadly, treatment of uncertainty.
Christos Maravelias
[email protected]
About the Author
Béla Lipták
Columnist and Control Consultant
Béla Lipták is an automation and safety consultant and editor of the Instrument and Automation Engineers’ Handbook (IAEH).