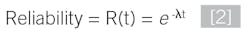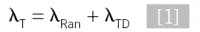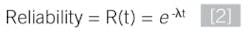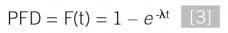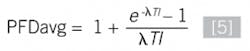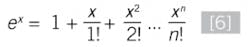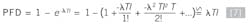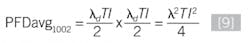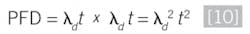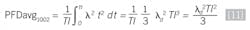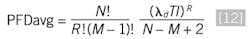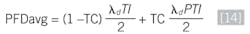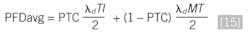The ins and outs of safety integrity level reliability calculations
One of the key elements required in the design of safety instrumented systems (SIS) is the engineering calculation of a reliability figure of merit called the safety integrity level (SIL) to determine if the designed SIS meets the target SIL as specified in the system’s safety requirement specification (SRS).
IEC 61511-1, Clause 11.9.1 requires that the calculated failure measure of each safety instrumented function (SIF) shall be equal to, or better than, the target failure measure specified in the SRS. Safety reliability calculations for low-demand systems relate SIL to the calculation of the probability of failure on demand average (PFDavg) or a required risk reduction (RRF). For SISs where the demand rate is more than one per year, or for high or continuous demand systems, the average probability of failure on demand per hour (PFH) is used.
SIL calculations have received considerable coverage in the efforts of the S84 committee of the International Society for Automation. The group’s ISA TR84.00.02-2015 technical report covers current industry practices, with a new version due to be issued in the near future. As an industry, we've been doing these types of calculations since the beginning of the SIS standards. And, while not rocket science, they can be a complicated subject. It's beyond the scope of this article to cover this subject in depth. However, we will cover some of the basics and some advanced topics where work is being done in this area.
All SIL calculations are based on statistical models. What we need to ensure is that the models are representative and not so complex that their usefulness is diminished. They can give us a reliability figure of merit to work with and help us better understand the system from a reliability perspective. These calculations are a verification tool to help design a SIS that has a high expectation of providing the required safety integrity level reliability as specified in the SRS, and meet verification requirements required by the IEC 61511-1 standard.
From a practical perspective, the calculations can provide an analysis of the SIS conceptual design, and help determine options to meet the SIL and at what proof-test interval. These calculations, unfortunately, can be subject to abuse if calculation parameters are cherry picked. To combat this potential abuse, architectural constraints (hardware fault tolerance requirements) are in the standard to help ensure the proper level of redundancy in the SIS design.
Primary methodologies
Most people use a commercial program to do SIL calculations, but one should always understand the underlying methodologies, their benefits and limitations. There are three common and generally acceptable calculation methods: simplified equations, fault-tree analysis (FTA) and Markov modeling. The reliability block diagram is sometimes used, but to a lesser extent, as are some other methodologies such as Petri nets.
The simplified equations are the simplest to understand and the easiest to implement in a spreadsheet, while the Markov model is the most complex. All will get the job done. The FTA and Markov model methods are graphical in nature, but the graphical Markov model can be quite complex. This makes the FTA a better approach if a visual representation is desired, particularly for analysis of complex systems. Further, FTA can typically provide a more detailed system design analysis. The main discussion in this article is based on simplified equations for low-demand systems in order to cover the main discussion points without digging into the complexity of all the varied methodologies. A more detailed discussion on various calculation methodologies can be found in references 1, 2 and 3.
Failure rates
We estimate the failure rates of instruments and devices based on the number of failures in a group of hopefully representative instruments over time. We then use these failure rates in our calculations for designing the SIS for our applications. We assume that our instruments will have the same or better failure performance than the group of instruments that the failure rate is based on.
Unfortunately, there are a number of failure-rate database sources, as well as many approval reports to choose from, which can give substantially different failure rate numbers (as discussed in reference 4). The selected failure rates for the calculations should also reflect reasonable failure rates expected for the type of service the instruments will be installed in. Unfortunately, the service used to develop database failure rates is often not well known, so for severe or difficult applications, failure rate numbers may not reflect actual performance.
Failure rates can be broken down into different types depending on what parameters are used in the calculation [1]. For simplicity of discussion, the failure rates in this article are divided into two types, dangerous and safe. The accuracy of the failure rates depends on the component design and construction, its application, its service, and the environment in which it's installed and maintained. The failure rate can have a significant uncertainty associated with it, which needs to be accounted for in the calculations, per IEC 61511-1. The key is the selection of a failure rate that's representative of the device’s inherent reliability and service where it will operate.
Many of the example PFDavg equations for redundant configuration are based on the identical instruments in the redundancy equation, but they can be easily extended to different instruments [9].
Generally speaking, all the math currently used is based on the concept of random failure as the primary failure mode, which follows the exponential failure rate distribution model, primarily due to the failure rate being considered constant during a device’s useful life for many of the devices in SIS service. The math lends itself well to the concept of periodic proof tests to calculate the PFDavg over the lifecycle of the SIS. In reality, the exponential failure rate distribution only applies well to electronic devices, and is less applicable to devices that are mechanical or have a significant portion that's mechanical, which can be significant for long test intervals. In those cases, the failure rate could be modeled as a random contribution plus a time-dependent contribution shown in Equation 1.
For an exponential failure distribution, it can be shown that the reliability for a one-out-of-one (1oo1) arrangement without consideration of common cause, diagnostic coverage, mean time to repair (MTTR) or other factors is:
And the failure probability is:
To determine the average PFD, the below equation for determining the average of a function can be used with the proof-test interval (TI) for t as the time period that the probability is averaged over:
After a little calculus:
This was painful enough; think about what the calculus for averaging with exponentials involves for redundant arrangements. There needs to be an easy way, and there is. We can use the Maclaurin series below to estimate the solution (1– e-λt) in a simpler form:
When the terms that don't significantly contribute to the PFD are removed (a good approximation is λTI < 0.1), this gives us the PFD, but we still need to get to the PFDavg. Why the average probability? This is because we're trying to calculate the probability of failure on a demand, but we don't know when the device will fail, nor when a safety demand will occur, other than for our calculation. We assume it can potentially occur during our defined test interval, making the average a better predictor of the probability of a failure during the test interval.
We can find the PFDavg by integrating to find the average of 1oo1 configuration with respect to time:
Now when we look at the PFDavg of a redundant arrangement, we have two options. The “average before” option, where the average probabilities of failure (PFDavg) for each redundant element are calculated before they're multiplied together, or, “average after” option, where the probabilities are averaged after the PFDs are multiplied together. Both methods are acceptable, but each gives a different answer. The “average after” method provides the more conservative answers and is commonly used in industry. This same question will come up when you're using FTA that uses the “average before” method, when you have redundancies that use an AND gate or a voting gate.
For example, for a 1oo2 arrangement with same type of instrument, if we average before we multiply the individual PFDs, we get:
While for a 1oo2 arrangement of instruments, if we average after we multiply the individual PFDs, we get:
If we extend these equations to a general “average after” equation for MooN redundancies, we get:
Where: R = N – M + 1.
The PFDavg calculation for the system must include all the components that could have a dangerous failure and defeat the SIS. These basic, simplified equations, however, don't tell the whole story, particularly when we're talking about redundant configurations.
Common cause
For redundant configurations, the potential for a common-cause failure (CCF) can significantly contribute to the PFDavg. CCF is a term used to describe random and systematic events that can cause multiple devices to fail simultaneously. The likelihood of multiple failures becomes more likely as the proof-test interval gets longer. In simplified equations, the probability of a CCF is commonly modeled as a percentage of the devices’ base failure rate (the term β is commonly used for this percentage), and the CCF probability contribution is added to the redundant PFDavg. For a MooN low-demand configuration, the general equation for redundant components with the common-cause contribution is:
[Eq 13]From this equation, we can see that common cause can easily dominate the equation if β is large enough. If the CCF is significant, it may be better to improve the design with diversity, rather than compensate by calculation. In addition, the determination of β is an estimate that can have a significant uncertainty associated with it.
Partial testing
There are several, general types of partial testing that affect SIL calculations. The first is where a defined portion of a proof test is performed online with the balance of the test performed offline. The purpose of partial testing can be to meet a PFDavg or allow lengthening the offline proof test interval. The primary example of this is partial-stroke testing of shutdown valves. For a 1oo1 valve configuration, the
PFDavg equation is:
Where: TC = test coverage, TI = manual proof test interval, PTI = partial test interval and λd = dangerous failure rate.
Another type of partial testing results from imperfect proof testing, which is where the SIS proof test doesn't fully test for all the dangerous failure modes. IEC 61511-1 requires consideration of proof-test coverage in the calculations. The percentage of dangerous failures detected by the proof test is called the proof-test coverage (PTC). This effect of this on the PFDavg can be calculated as follows:
Where: PTC = proof-test coverage, TI = manual proof test interval, MT = mission time (interval point where the SIS is restored to original, full functionality through overhaul or replacement) and λd = dangerous failure rate.
Note that using this calculation is essentially adding a random failure probability to a failure probability caused by a systematic failure, which is sort of like adding apples and oranges. When the result is within an acceptable SIL band, this can result in the plant living with a percentage of undetected dangerous failures that aren't tested for over the mission time.
Would you want to do this? If the calculation results in moving outside of the acceptable SIL band, what do you do? One poor design choice is to test the things you're already testing more often to make the PFDavg fit the desirable SIL band (e.g., using the random part of the equation to fix a systematic problem). This seems contrary to designing a reliable SIS system. Rather, the best approach is to improve your PTC or at least reduce mission time.
Diagnostics is another form of partial testing where the failure rates are divided into failures detected or not detected by the device’s internal diagnostics or external diagnostics. The effect of this on the PFDavg can be shown using equation 14, where the diagnostic coverage (DC) is substituted for the TC and the diagnostic test interval for the PTI. This equation can be used to cover external diagnostics in FTA. Care should be taken where credit is given to the diagnostics to improve the PFDavg that dangerous detected failures are converted to “safe” failures by the design of the system. The TC, DC and PTC are estimated values, and there's an uncertainty associated with their determination.
Site safety index
Site safety index (SSI) is a quantitative model that allows the impact of potential “systematic failures” like poor testing to be included in SIL verification calculations. SSI has five levels from “SSI-0 = none” to “SSI-4 = perfect,” and the use of SSI in the PFDavg calculation results in a multiplicative factor where anything less than SSI-4 will cause the PFDavg calculation to have a higher PFDavg than the basic calculation. (5)
Again, using this kind of model to compensate for poor systematic performance rather than improve that performance seems contrary to designing a reliable SIS and the work processes that support that reliability.
Proof test intervals
The off-line proof test interval is a key parameter and is typically selected based on a turnaround frequency, while the on-line test frequency, if any, is typically determined by the PFDavg requirements. In practice, turnarounds typically occur in the year they're projected, but can vary within that year due to operating and economic conditions. If your plant turnaround schedule has varied historically, an analysis of the effect on the PFDavg should be done.
Uncertainty
Stronger considerations of the uncertainty associated with SIL calculations is a major addition for the next edition of the ISA TR84.00.02 technical report. We must recognize there's uncertainty associated with the reliability parameters. 61511-1 states, “The reliability data uncertainties shall be assessed and taken into account when calculating the failure measure.” The technical report provides a number of ways to compensate for uncertainty, primarily for the failure rate, which are mentioned below, but a detailed discussion is beyond the scope of this article.
Two methods that have been used to compensate for uncertainty are to set a value for the target PFDavg that shifts the target PFDavg to a more conservative value (e.g. applying a safety factor) and variance contribution analysis. These methods, plus the use of CHI-squared distributions are discussed in References 1, 6 and 7.
One could also use a Bayesian approach with field data or other data sources to improve the failure rate parameters, which is discussed in Reference 8. Also, see Stephen Thomas’ discussion of this and other SIS topics, which can be found at his www.SISEngineer.com website.
Relevance of SIL calculations
SIL calculations are an engineering tool that can assist us in the design of SIS and is required by IEC 61511-1. But they're not the end all in designing a reliable SIS. There's an ongoing trend to consider additional factors in the calculation—leading to more complex calculations—with the assumption that if we factor in more things, we'll get a more accurate result, leading to a better design. However, this may not always be the case. Consideration of these additional factors typically results in a higher PFDavg, which when the PFDavg crosses the SIL lines, leads to changes in the design or the test frequencies, but not necessarily a more reliable system. Consideration of the additional parameters can also be abused to compensate for a bad design by allowing a poor design to remain if the calculation doesn't drop you down a SIL band.
Many of these factors also involve mixing random failure with systematic failure in the calculation, which can lead to fixing the systematic portion of the calculation by modifying the random portion, which doesn't fix the problem. An example can be “fixing” poor proof-test coverage by testing the system more often, which still leaves the dangerous failures not tested for still hanging out there, latent, to come back and haunt you. The solution is to improve the test coverage and not compensate for it.
Uncertainty is another area where having poor data is compensated for by increasing the failure rate. This can result in added redundancy or more testing, but doesn't fix the inherent problem of having bad data to begin with.
SIL calculations should never be used to compensate for a bad design. Consideration of these additional factors shouldn't be used to compensate for a poor design, but rather to identify areas where the design needs improvement.
While there is a need to achieve a quantitative metric for a SIL rating based on the IEC 61511-1, one should use common sense and good engineering practice in these calculations. Remember, a reliable system will always result from an improved design, rather than accepting a less reliable system that the calculation says is acceptable. Calculations should be used as a tool that helps lead to a reliable design, and not the sole “proof” that you've achieved one.
References:
- ISA TR84.00.02 – Safety integrity level (SIL) – verification of safety instrumented functions," 2015, current draft.
- Safety instrumented systems – a lifecycle approach, Paul Gruhn, Simon Lucchini, ISA, 2019.
- Safety instrumented system verification, William M. Goble and Harry Cheddie, ISA, 2005.
- “Will the real reliability stand up?,” William L. Mostia, Jr. PE, Texas A&M
- Instrument symposium for the process industries, 2017.
- “Assessing safety culture via site safety index”, Julia V. Bukowski, Denise Chastain-Knight, 12th Global Congress on Process Safety, 2016.
- “Evaluation of uncertainty in safety integrity level calculations,” Freeman, Raymond and Angela Summers, Process Safety Progress, Wiley, 2016.
- “General method for uncertainty evaluation of SIL calculations – part 2, analytical methods,” Raymond “Randy” Freeman, American Institute of Chemical Engineers, 2017.
- “A hierarchical bayesian approach to IEC 61511 prior use,” Stephen L. Thomas, P.E., Spring Meeting and 14th Global Congress on Process Safety, 2018.
- “Easily assess complex safety loops,” Dr. Lawrence Beckman, CEP, March 2001.
About the author
Frequent Control contributor William (Bill) Mostia, Jr., P.E., is prinpal, WLM Engineering, and can be reached at [email protected]