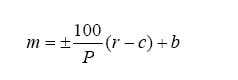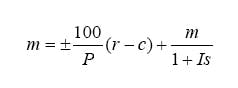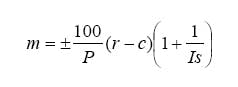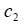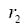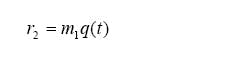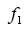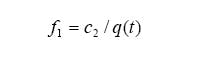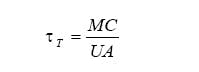The Integral mode of a controller is essential in eliminating offset in any loop subject to load changes—which is almost every loop encountered in process control. Consequently, almost every controller has integral action in one form or another.
However, tireless effort to drive deviation between the controlled variable and its set point to zero presents problems when the loop is open. In an open loop, no amount of control effort will be successful, and continuing to integrate results in “windup” with adverse consequences. The integral component in a “wound-up” controller doesn’t balance the process load, driving the controlled variable away from a steady state when the loop is eventually closed. This imbalance can produce a large deviation, requiring integral action to eliminate, and, if repeated, it results in a limit-cycle immune to correction by tuning the controller. Preventing windup requires reconfiguration of the controller, and external-reset feedback is the most satisfactory method of accomplishing it.
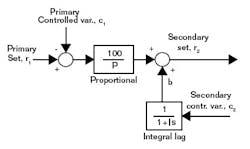
The first pneumatic controllers had only on-off action. A mechanical linkage, whose position represented the difference between process measurement and set point, acted on a relay to switch the output pressure between its two states. Proportional control was introduced by negative feedback of that pressure to reposition the linkage through a bellows. The precise value of the output when the deviation was zero could be adjusted by a screw, acting on a spring opposing the bellows, as a bias (Equation 1):
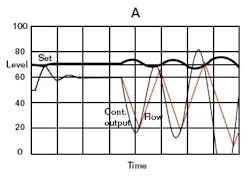
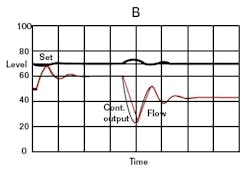
Proportional offset develops whenever the process load requires a value of controller output that isn’t equal to the bias. Consider, for example, a proportional-level controller with a 50% bias manipulating the flow entering a tank. If the flow leaving that tank exactly matches the flow entering with the valve 50% open, there will be no offset. However, at any other value of outflow—which requires a matching inflow to reach a steady state—the matching inflow can only be attained by a proportional offset.
In applications where offset was particularly undesirable, a plant operator might reset the set point to position the controlled variable where it was wanted. The offset remained, however, and it was variable. It could be manually eliminated by operator adjustment of the output bias, and this became known as manual reset, but only until the load changed again.
In 1929, “Doc” Mason of the Foxboro Co. came up with the idea of replacing the bias spring with a bellows connected to the controller output. If the bias and controller output could be kept equal in the steady state, Equation 1 shows the offset will be zero. This became automatic reset.
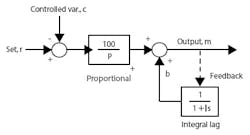
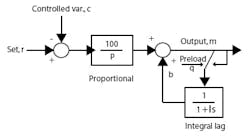
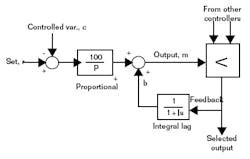
However, simply connecting the two bellows together produces an on-off controller, as the new bellows adds positive feedback to the controller canceling the negative feedback of the proportional bellows. To stabilize this loop, the positive feedback has to be slower than the negative feedback coming from the process. So, a restrictor was inserted between the controller output and the feedback bellows, creating a first-order lag. Initially the restrictor was fixed, then a selection of fixed restrictors was used, and finally an adjustable restrictor. The configuration is shown below in Figure 1, in which time constant “I” was known as the reset time.
FIGURE 1: AUTOMATING RESETThe reset feedback path in Figure 1 is shown as a dashed line, indicating that it can be broken to stop integration, and prevent windup for reasons explained in the various applications below. Not all controllers integrate by means of a feedback loop, however, and these require other methods of windup protection that aren’t as effective. So, it may be necessary to build a controller from the elementary function blocks shown in Figure 1 to obtain the capability of external-reset feedback.
Batch Control
An early problem caused by integral windup was temperature overshoot in heating batch reactors. The reactor was charged cold, with the temperature controller in automatic, set point at its desired value, and the steam block valve closed. Opening the block valve started the heating operation. At this point, the reset bellows contained full-supply pressure, keeping the controller output saturated and the steam control valve wide open until temperature crossed its set point. The resulting overshoot was unacceptable. The remedy shown below in Figure 2 breaks the reset-feedback path by a batch switch whenever the controller output exceeds 100% or wherever the manipulated variable limits, and substitutes a manual-loading signal. Suitable adjustment of this preload positions the integral term near the anticipated process load, which can prevent overshoot, and provide a smooth transition from proportional or proportional-plus-derivative to PI or PID control. This same method is now applied to digital controllers with external-reset capability.
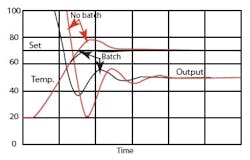
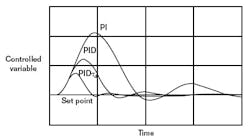
Figure 3 shows how an unprotected (no-batch) PID controller can cause temperature overshoot during startup of an inert batch when the integral term is saturated at 100%. Derivative acting on the controlled variable causes the output to leave its limit before set point is crossed, but not soon enough to avoid overshoot. In an exothermic reaction, the overshoot would be even more severe, and could result in product loss. The controller protected by a batch switch is preloaded near the anticipated load of 50%, where split-range heating and cooling valves are both closed, thereby avoiding the overshoot. The controller’s mode settings can be tuned for optimum load rejection, and the preload adjusted to produce the desired approach to set point on startup. Too low a setting results in undershoot, and too high a setting causes overshoot. A preload setting of 100% would produce the same overshoot as the no-batch controller in Figure 3.
FIGURE 3: AVOIDING OVERSHOOTProper preloading of the batch switch optimizes the approach to set point.
While the loop is open, if the deviation happens to lie within the proportional band of the controller, its output may fall below the switch setting after transfer to preload. Then, the switch will reverse position, and integration will resume, driving the output back to the switch setting. The switch will then cycle between its two positions. In a digital controller, this reversal could happen at every scan interval. The ultimate effect is essentially to control the controller’s output at the switch setting, with the integral term “b” settling at an intermediate position representative of the current process load. Any upset reducing the deviation will then be countered by an immediate change in controller output away from the limit. This behavior is common in anti-surge compressor control, where suction flow is normally well above the surge set point and the recycle valve is held closed by the flow controller. A sudden loss in load will reduce flow, and the controller must start opening the recycle valve before the set point is reached.
The batch switch applies equally well when the manipulated variable encounters a lower limit. The switch then transfers to preload when the controller output falls below that lower limit.
Override Control
Override control was recently described recently in H. L. Wade’s “Under the Hood of Override Control, Part 1 and Part 2,” CONTROL, Dec. ’05 and Jan. ’06. In these systems, two or more controllers compete for the same manipulated variable, which is selected based on whichever has the lower or higher output. Since only one controller can be selected at any given time, the remaining loops are open, and their unselected controllers will wind up unless protected.
Figure 4 below shows the most effective method for avoiding windup in the unselected controllers: the selected output is the common feedback signal to all of the controllers in the system. Simply stopping integration in the unselected controllers isn’t enough because it leaves their integral term loaded with a constant that loses its relationship to process load over time.
FIGURE 4: PREVENTING WINDUP
The selected output, however, represents current process load, and therefore keeps the unselected controllers current while their loops are open. Only the selected controller sees its own output fed back, and so it alone integrates. Because all controllers are biased at the same level, transferring control from one to another will tend to take place when both are at zero deviation, and it therefore becomes a smooth event.
The integral lag plays an important role in this transfer. Other methods of windup protection tend to be too abrupt because they include forcing all controller output limits to track the selected output or periodically initializing the unselected controllers. Any noise on the selected output is easily rectified into a bias with these methods, potentially shifting the transfer point on the unselected controllers, or causing offset in the selected controller. The integral lag avoids this problem by effectively filtering noise.
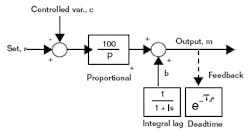
Deadtime CompensationAccess to the reset-feedback signal allows insertion of deadtime compensationFor example, this controller’s performance is shown in its simulated step-load response curve in Figure 6, compared to the curves of PI and PID controllers tuned to minimize integrated absolute error (IAE). Its integrated error is only 40% that of the PID and 14% that of the PI controller, while its proportional band is less than half of the PID and a third of the PI controller. What’s even more remarkable is that the process being controlled in this simulation is a distributed lag, containing no deadtime at all! Its dynamic response is typical of heat exchangers, stirred tanks, and distillation columns, consisting of multiple lags distributed throughout their mass.
FIGURE 6: MINIMIZING IAECascade Control
Perhaps the most valuable role of external reset is in cascade control. The two controllers have demonstrated difficulty in transferring from full-manual to full-automatic operation. And, whenever the secondary controller is placed in manual or reaches an output limit, the primary controller winds up. This is solved with the configuration shown in Figure 7.
Observe that the entire secondary loop, including the secondary part of the process, lies within the integral term of the primary controller. This turns out to be a distinct advantage. When a deadtime block was inserted in the integral feedback path, the performance of the controller improved markedly. The secondary loop now inserted in that path may include some deadtime and other lags, which also improve the performance of the primary controller. Not only does this configuration allow the integral time of the primary controller to be reduced, but also allows its proportional band to be reduced.
Adding deadtime to a controller was found to reduce its robustness, which is the ability of the control loop to remain stable while process parameters vary. However, including the secondary loop in the primary integral path actually improves robustness because it includes some potentially variable process parameters. The thermal time constantAccommodating Velocity Limit
The velocity-limit or rate-limit property of a final element can pose a danger to a control loop, if the integral time of the controller is shorter that the stroking time of that element. However, the danger is hidden while the loop is operating around set point because the actuator takes little time to move only a short distance. When a sufficiently large disturbance strikes, the actuator may fall behind the controller output enough to cause more integral action and further falling behind. This triggers an expanding cycle (Figure 8A) that requires operator intervention to stop.
Figure 8A is the simulated response of a level-control loop, where the integral time of the controller is set at half of the stroking time of the valve actuator. The first disturbance is a step-load change of 10%, which isn’t large enough to destabilize the loop. Next, a 17% step is large enough to trigger the expanding cycle. This is particularly insidious behavior because the response of the loop to normal variations in load is quite acceptable, which gives false confidence, while masking a potentially fatal instability.
The ideal correction is to speed up the actuator, but this option often isn’t available. The simplest remedy is to increase integral time until the loop is stable following the largest conceivable disturbance. This requires extensive testing, and may not provide complete assurance that the cycle won’t recur. It also degrades the performance of the controller in response to normal low-level disturbances because integrated error varies directly with integral time.
External-reset feedback of the measured position of the final element can eliminate the danger without compromising controller performance. In Figure 8B, the actuator’s actual position is fed back to the integral term of the level controller, with the disturbances repeated. Integral action is now paced to the actuator’s movement, which avoids any risk of an expanding cycle, no matter how large the disturbance or how slow the actuator. This is simply the same principle applied to cascade control in Figure 7. To avoid offset there must be a secondary controller to force the final element to follow the primary output precisely in the steady state.
The need for external reset became clear during a recent startup of a nuclear power plant, where the level in a boiling-water reactor was controlled by manipulating the speed of up to three feedwater pumps. The integral time of the feedwater flow controller was set at 0.18 min, the expected rate limit of the pump-speed governor. When first operating with one pump on line, control was acceptable, until a disturbance triggered an expanding cycle. Review of the records indicated a much slower response of pump speed than expected, requiring an integral time in the flow controller of 1.6 min to stabilize, which was unusually high for a flow loop.
Oddly, the dynamic causing the cycle disappeared when multiple pumps were on-line, so the problem is a variable one. The solution is external-reset feedback of measured pump speed to the flow controller, allowing it to integrate as fast as pump speed can follow. Implementation is complicated by the use of three pumps, with their characterizers. To avoid offset, all calculations performed in the controller output path have to be reversed in the feedback path as described earlier for feed-forward control.
| About the Author |

Leaders relevant to this article: