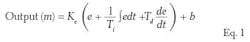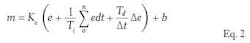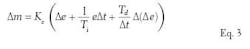Q: The control system I am working with does not have external reset, but I was wondering if there is a way to create an external reset on a standard PID feedback controller by setting integral to zero (with I = 0) and a first- order lag block. The PID controller would also need to have feed-forward capability to accept the external reset signal.
I have made some attempts to read the output from the controller, pass that through a first-order filter, and then feed that back in to the feed-forward connection of the PID controller, but it does not work right. I am wondering if you have ever done this or if you know how it can be done.
The control system I am trying to do this on is an HC900, which is a stand-alone, very small-scale Honeywell hybrid controller. The function blocks are rather simple (weak), and that is why I am wanting to create my own external reset controller.
John McIlwain
[email protected]
A: For the benefit of the less experienced readers, before answering your specific question, I will briefly explain the basics about PID, feed-forward and external reset.
In a proportional-integral-derivative (PID) controller, the output signal to the control valve m(t) is the sum of four components (Eq. 1):
The four components are:
- The live zero or bias (b),
- The proportional contribution which is a function of the present error, P = Kc(e),
- The integral contribution which reflects the area under the error curve and responds to this error that was accumulated in the past during the integral time Ti. The integral contribution is I = Kc(∙edt/Ti).
- The derivative contribution, which is a function of the projected future error, if the present direction and rate of error change continues for a period set by the derivative time Td. The derivative contribution to the total output signal to the valve is D = Kc(Td)(de/dt)
The analog PID algorithm can be the "standard" (see Equation 1), interacting or parallel (shown in Table 1), or can be more sophisticated, such as the ones that take the dead time (Td) of the process into account, etc.
Similar to the analog algrorithms, there is also a wide variety of digital PID algorithms, but basically they can be grouped into two categories: positional, where the total output to the valve (m) is recalculated after every cycle (see Equation 2),
or velocity, meaning that the previous value of m is held in memory during the cycle, and only the change that occurred since the last cycle period is calculated (see Equation 3).
Naturally there are other variations, but for our purposes here, this is enough.
Now, after this brief summary of the PID algorithms, let us look at feed-forward (FF), the purpose of which can be easily understood by thinking of a heat exchanger where our goal is to control the outlet temperature (To). In that case, if either the inlet flow (Fi) or the inlet temperature (Ti) changes, without FF, the PID controller would not know that the load changed until the water passed through the exchanger and, therefore, on every load change an upset would occur. The larger the volume of the exchanger, the larger this upset would be.
FF mostly eliminates this upset by anticipating this "load change error" and compensating for it immediately when the load changes. The FF correction is made by subtracting the Ti from the PID output signal(m) and multiplying that difference with Fi, so that the new output becomes m = Fi{m-Ti). The Fi in this FF algorithm is usually "lead-lagged." This is because if the load rises, beside the heat balance, additional heat is needed to increase the temperature of the mass of the exchanger itself. This is "lead." "Lag" is the opposite effect that is needed when the load drops.
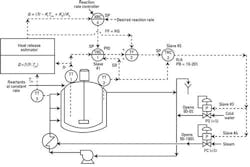
Now let us see what external reset (ER) does and why it is needed. In a cascade loop, for example, it is needed, because without it, when the operator switches the master (TRC-1 in Figure 1) to manual, this TRC would keep integrating the error ("would wind up"), because it is not able to affect its own measurement (T2), as its output is blocked. ER eliminates this problem because it arrives from an "unblocked" source: the measurement signal to the slave controller (TRC-2). Therefore, the ER stops integration of the error in TRC-1 whenever the slave is not on setpoint (such as under manual), and thereby converts the integral contribution to a constant bias.
Figure 1: This control system has both feed-forward and external reset, serving to keep the reaction rate constant in a variable reaction temperature process.
As to the value of having both FF and ER, refer to Figure 1. Here, the goal is to keep the reaction rate of a batch reactor constant by calculating an FF input, and sending it into summer TY-2, while ER is provided by the measurement signal of the slave (TT-2) to the master PID controller TRC-1.
Sorry for this long introduction, which I believe was necessary for the benefit of some readers, and now coming to your question of how to create an ER if the digitally implemented PID does not have a "connection" for this input. The question asked is: would setting integral to zero (with I = 0), and sending a signal generated by an external first-order lag block to the FF "input" do the trick?
As you can see in Figure 1, FF is basically a bias on the output of TRC-1. So, in effect, what is being asked is can one send the ER signal on Figure 1 through a first-order lag and then to TY-2, where previously the FF signal was introduced. The answer to this question is very much a function of the particular DCS algorithm used, and I will let Dr. Harold Wade and other colleagues explain that in more detail in their answers below.
Béla Lipták
[email protected]
A: Regarding your inquiry about constructing a controller with external reset feedback, using a PID with feed-forward capability and a first-order lag block; I have not done this, but I have built up an external reset controller from function blocks in my own simulation and training software (PC-ControLAB).
I don't know why you could not get your system to work right, so I will start off making suggestions.
First, you mention setting I = 0. With some systems, that means "turn the integral mode off." Then that setting should work. With some systems that means "set the reset, in Repeats/Min (not Min/Repeat) to 0," which effectively turns the integral mode off. In either of those cases, we're OK so far.
With the system you are using, how is the feed-forward combined with the PID algorithm? With some systems, the feed-forward signal operates in an incremental mode, rather than a position mode. The PID portion of the algorith calculates how much it wants the controller output to be, then it adds (or subtracts) an incremental change wanted by the feed-forward signal. On other systems, both the PID portion and the feed-forward portion operate in an incremental model.
If you're using this for external reset feedback, you must be very careful about how the feedback (essentially the proportional mode of the controller) and external reset signal are combined. In my ISA book (Wade, H. L., Basic and Advanced Regulatory Control: System Design and Application, 2nd ed, ISA, 2004), I compare several methods of combining used by various manufacturers, and come to the conclusion that the position form, mimicking what was done 40 to 50 years ago with pneumatic controllers (that is, during my time with Honeywell), is the best. I even have a statement in my book disagreeing with a statement in IEH3 that says with significant different integral times, it is better for the external reset feedback to bypass the first-order lag whenever a particular controller is not selected. I state that after extensive simulation, I did not find this to be true.
I did not even get into the subject of how to handle manual to automatic transfers. Especially with a build-up selector control system, that could be a whole separate chapter.
Harold Wade
www.wadeco.com
A: In theory, your approach makes sense, but there may be problems with implementing with standard blocks. For example, will it initialize correctly? Will it perform correctly with the built-in windup logic of the control system (which might freeze integration in a direction that would cause windup)? External reset feedback is a positional algorithm, but your system may be velocity-based, so there might be a problem there.
In the book, Design of Distillation Column Control Systems by Buckley, Luyben and Shunta, Butterworth-Heinemann, 1985, an external feedback arrangement with derivative action and feed-forward control is described.
In general, one thing that practitioners need to be aware of is that some systems may use the term external feedback, but it can have a different meaning from what is described below and used by Greg Shinskey, Harold Wade and others. It is amazing to me how many systems there are that do not support external reset feedback.
Mark Darby
[email protected]
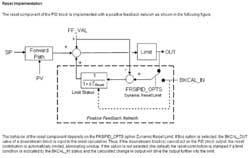
A: Some manufacturers provide external reset capability, but give it a different name. For example, in Provox this capability was called integral tracking; in DeltaV external reset is exposed through the Dynamic Reset option. If the HC900 has basic function blocks, then you should be able to implement a PID with external reset and feed-forward capability. The following shows the basic implementation.'
Terry Blevins
[email protected]

Leaders relevant to this article: