Can Ziegler-Nichols equations be used to tune non-interactive controllers?
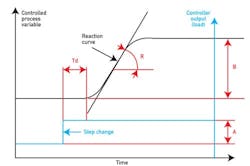
The dynamic response of a self-regulating process to an upset (a step change in load or setpoint) can be described by its reaction curve, where A is the size of a step change in setpoint (load); B is the steady-state full response of the controlled variable to A; B/A is the process gain; R is the reaction rate (speed of response); and Td is the dead time–the time it takes before the process starts to respond.
Q: Thank you for your contributions to our industry. I have learned much from reading your articles and columns. I have a simple question to which I have not found a definite answer.In general, using the Ziegler-Nichols (Z-N) equations, we can calculate a starting set of tuning constants. My question is, are the calculations based on interacting controllers? Can they be used for non-interacting controllers? If they have been developed on non-interacting controllers, can they be converted for tuning interacting ones?
Some references and text books state that the Z-N equations are for non-interacting controllers, but I have read that the interactive controller was used, and that you can use conversion tools. What do I tell students? I'm tending to say that Z-N was developed using an interactive controller, and they would need to convert to a non-interacting form.
Don Lovell
[email protected]
A: Your question concerning the Ziegler-Nichols controller is fully answered by a dozen excellent comments given below by my expert colleagues. Therefore, I will not focus on this narrow topic, but will say a few words about tuning itself and about what has changed since we entered the digital age.
Tuning a controller is like teaching a pilot how to keep his/her vehicle on course. This requires that the "personality" of the controlled process (the vehicle) be fully understood by the pilot (the controller). The dynamic response of a self-regulating process to an upset (a step change in load or setpoint) can be described by its reaction curve (Figure 1). When a programmer at a DCS supplier of, say, Foundation fieldbus, or at a PLC supplier is preparing a tuning algorithm, he or she assumes that all that is needed is the data I show on Figure 1 (A/B, Td and R) to calculate the required settings for the controller's gain ("P," which responds to the present error), for integral ("I", which considers the error accumulated in the past), and for derivative ("D", which predicts what the error would be in the future if not corrected). When done, programmers think that the job is done. In a way, they are correct, because that is all that a programmer is qualified to do.
This is the point where the role of the process control engineer starts. Why? Because most processes are not that simple. When we are controlling a nuclear reactor or a fracking process, etc., the values of B/A, Td and R are not constants, but variables for many reasons: Because PID loops interact and each has its own safety limit; because some of these loops are not self-regulating; because the continuous measurements of B/A, Td and R are difficult, if not impossible, to obtain; because noise prevents accurate measurements, etc., etc. Therefore, the duty of our profession is to understand this. If automatic control does not work, the system will be switched to manual and will not only operate at low efficiency and produce low quality products, but in critical processes, safety will be lost.
Therefore, we must understand that the process must be fully understood before it can be controlled (and a programmer is not qualified to do that), and that the respect for and recognition of our profession will not grow, unless we, the process control engineers, take on the responsibility to check and modifying the programmer's algorithms as needed.
Béla Lipták
This column is moderated by Béla Lipták, automation and safety consultant and editor of the Instrument and Automation Engineers' Handbook (IAEH). If you have an automation-related question for this column, write to [email protected].
A: The Z-N tuning rules were developed on a Taylor Fulscope controller, which was interacting with parallel feedback of the output to the integral (I) and derivative (D) restrictors. This compares to the Foxboro Model 40 controller which had a serial feedback connection through the two restrictors. (Foxboro patented the serial configuration.)
For both controllers, the effective value of integral time was the sum of the two time constants: D + I, and the effective value of the derivative time was 1/(1/D + 1/I). For the Foxboro controller, the effective proportional gain was K(1 + D/I), but for the Fulscope controller it was K(1 + D/I)/(1 - D/I).
The last term had a powerful effect as D approached I, and if D > I, the controller would work backwards. Hence, Z-N settings fixed the D/I ratio at 1/4, whereas more like a ratio of 1/2.5 was optimum with a Foxboro controller; the M-40 had a mechanical stop that prevented D from exceeding I.
This is covered in some detail on pp. 71-73 of my book, Feedback Controllers for the Process Industries, McGraw-Hill, 1994, under the heading of "Single-Stage Interacting Controllers."
Greg Shinskey
[email protected]
A: Ziegler-Nichols tuning was developed for pneumatic controllers in the 1930s. Those controllers were entirely mechanical—a set of links, levers and bellows designed to provide proportional control with reset and anticipatory control when needed. I use these terms because pneumatic controllers did not solve an equation. In fact, the earliest digital control on computer-based direct digital controls made special attempts to derive the PID equation by digitally simulating the behavior of pneumatic controllers. When they did this, the form of the equation that resulted looked like this:
m = Kp {1/Ki ∫e dt + Kdde/dt}
They called this the "non-interactive" form of the equation, but clearly since Kp is a multiplier of both the integral and derivative terms, it is highly interactive. Nevertheless, this is the form of the equation used for all digital control: DCS, digital single-loop, computer control, and Foundation fieldbus.
The other form of the PID equation with three clearly independent terms is actually non-interactive, but is used by motion control, machining and rocket thrust vector control. It is implemented on all PLCs and variable-frequency drives. It is used for process control with about the same results as for the "non-interactive" equation, but as you can tell, the results are slightly different. Z-N tuning is used for both equations and gives an excellent starting point. Please do not regard Ziegler-Nichols tuning constants as theoretical optimums. They are not. They are just a good starting point for loop tuning.
Dick Caro
[email protected]
A: Most assume that it was based on the interactive form, since it represented the implemented form of the PID algorithm in the pneumatic Taylor controller. However, the tuning works better for the non-interacting form. But we really don't know for sure, and most references don't identify the equation form. See Basic and Advanced Regulatory Control, 2nd ed. (ISA) by Harold Wade, page 132. However, fairly recent work (Hellem, 2001, referenced by Skogestad ) concluded it was likely based on the non-interacting form, the reason being that the ideal form was likely used in the numerical simulations performed on an electronic computer.
Of course, for PI control, it makes no difference.
Mark Darby
[email protected]
Aslo Read "Don't Over Look PID in APC"
A: The integral and derivative actions for pneumatic controllers were interactive because of mechanical constraints in the design (i.e., capacitance bellows and restrictors). When Ziegler and Nichols came up with their pneumatic controllers, PID or otherwise, did not exist. Hence, I do not believe that they had interacting PID in mind at all!
The only possible reason to convert to interacting is when you are upgrading pneumatic controllers to modern digital control. You could then start with the existing PID tuning settings. Modern controllers have the interacting option just for these historical reasons.
However the integral and derivative settings were so inaccurate on the old pneumatic controllers that I did not even bother with those settings. Hence I used the non-interacting version right from the start and retuned the controllers from scratch when upgrading pneumatic controllers. The proportional/gain settings were reasonably close. In other words, there is better value is retuning then wasting time with the interacting PID controller.
I would only discuss interacting PID in a historical context. I do not see any value in implementing interacting PID control.
Simon Lucchini,
[email protected]
A: Ziegler and Nichols developed their tuning rules and methods for a PID interacting controller, but this is only part of the story. The rules were calculated to accomplish good load rejection, not setpoint tracking. The process model used in all the testing was a lag-time-dominant; i.e., the process time constant is much larger than the process time delay. If you apply the rules to a time-delay-dominated process, the response is going to be really sluggish.
Ziegler and Nichols chose quarter-amplitude damping (QAD) as a performance metric (for reasons that are not known to me at least). QAD is a tuning that will give very narrow robustness margins, so the tuning, as calculated, is not likely to survive for a long time in an industrial environment.
As for the formulas to convert from interacting to non-interacting tuning parameters, they are really difficult to find once you know what the PID algorithm you are using is. You may find it to be impossible to find some of the tuning equivalents if D > 1/4.
The algorithm of the PID used by Ziegler and Nichols is u(s) = Kc*(1 + 1/sI)(1+sD/(1+a.sD)), where
Kc = Controller gain, dimensionless or %/% if you prefer;
I = Integral time, time units;
D = Derivative time, time units;
a = the inverse of the D maximum gain, typically 0.1
There are some other tuning rules out there, most people compare their methods against the Z-N method without even knowing what they published in their 1942 hallmark paper. Even if the QAD is not a good tuning criterion, the concepts that they presented have withstood the test of time. I just hope that your students will eventually be able to distinguish the good from the bad tuning criteria.
Hope this helps, Best regards,
Sigifredo Nino
[email protected]
A: Google led me to a web site that covers the ground very well:
http://blog.opticontrols.com/archives/287
Bill Hawkins
[email protected]
A: I believe the Z-N rules were developed for the interacting controller. Some textbook authors realized that and explain it; some do not realize it and propagate a tuning error.
The conversion rules to the non-interacting form are standard in many texts, and in my chapter in the Instrument Engineers' Handbook, Vol II, Process Control and Analysis, Rhinehart, R. R., H. L. Wade, and F. G. Shinskey, 4th Edition, B. Lipták, Editor, Section 2.3, "Control Modes—PID Variations," pp. 124-129, Taylor and Francis, CRC Press, Boca Raton, FL, 2005.
I don't like the common labels interactive or non-interactive. The interactive controller is also called the rate-before-reset (when you look at the Laplace block diagram), or physically realizable controller. In the pneumatic days of bellows and levers, it was a physically realizable construction of P, I and D modes. The physical limitation is not needed in today's electronic or digital world.
There is a standard form of the PID controller, which is variously termed non-interactive or parallel (when looking at the Laplace block diagram) in which the derivative time multiplies the derivative term only, and the integral time divides the integral term only. In the rate-before-reset (interactive version) the integral time and derivative time act on both terms and the overall controller gain. The interaction is a consternation, a confusion and in my opinion, not a good thing.
For control, it seems that "interaction" is something good, and "non-interacting" would be undesirable. But in my opinion, the interacting is undesirable, and the separation of function in the standard controller is what is desirable. I wonder if the labels were devised by those who wanted the rest of the world to hold onto the physically realizable legacy!
So I don't like to use the labels interacting and non-interacting.
Further, I don't like the Z-N rules. For my preference, the QAD (quarter-amplitude damped) target for a CV to follow a step in a setpoint is not a good measure of controller goodness in the process industry. It is more aggressive than makes me comfortable. It also doesn't de-tune a controller so that it remains temperate when the process gain increases.
Further, the Z-N ultimate method is wholly not permissible, in my opinion, in the process industry. Who would let someone upset a process like that? And the primitive methods to get FOPDT (first order plus dead time) models for the Z-N open loop method are time-consuming, require too many mathematical procedures to not make errors, and are inaccurate. Whether Cohn and Coon or whatever, I discourage such methods.
I think the ultimate method has the positive outcome as it is a basis for the ATV (auto- tune variation) method.
But my preference for tuning is heuristic approaches that get "good enough" in a quick time with minimal upsets. Unfortunately, most college professors do not like books that teach heuristics and require judgment. They want texts that have black-and-white mathematics for convenient testing of the students.
R. Russell Rhinehart
[email protected]
Also Read "Reader Feedback: Basic PID and Control Issues"
A: The interactive form is more properly called the series form. Nearly all controllers at the time of Ziegler and Nichols used the series form, except for some special offerings. If derivative action was used in the series form, the tuning settings had to be converted to the ISA standard form, also known as the non-interactive form. In particular, the series form allows, and some tuning methods even encourage, the use of a rate time greater than the reset time. The literal use of these series form settings in an ISA standard form can cause severe oscillations. Also, attention must be paid to the units of the settings, in that some companies use percent-proportional band instead of a dimensionless gain for the proportional mode, repeats per minute instead of seconds for the integral mode, and minutes instead of seconds for the derivative mode.
As a side note, Ziegler- Nichols settings were designed to minimize the peak error from a load disturbance and will cause a damped oscillatory response. To provide more robustness and a smoother response, the Z-N gain is cut in half. A setpoint lead-lag with lead set 25% of lag or 2 degrees of freedom (2DOF) structure with beta and gamma set to 0.5 are used to prevent overshoot from Z-N settings in a setpoint response. Also, the Z-N reaction curve method is more practical than the ultimate oscillation method because you can estimate the tuning settings from the delay and initial ramp rate. I have included the following info from my impending 4th edition of Tuning and Control Loop Performance to provide more information and background on ISA forms.
PID controllers developed before this century used the series form, also known as the interactive algorithm, where the derivative mode is computed first in series with proportional and integral modes. The series form minimized the cost and complexity of analog controllers. Early digital controllers retained this form to give the same feel in tuning and enable the use of the same tuning settings. Pneumatic and many electronic controllers actually used a positive feedback implementation of the integral mode on external reset feedback. The conventional integral mode depicted principally appeared with the advent of digital controllers, where an integrator could easily be implemented, coordinated and limited.
In the series form, the derivative mode result is the input to the proportional and integral modes. Its advantage is that interaction factors prevent the effective rate time from becoming greater than effective reset time that could cause instability. As the rate time setting increases, the effective gain and rate time decreases, and the reset time increases. The primary disadvantage of the series form is the lack of understanding of the interaction factors. There is also greater magnification of noise from the multiplicative effect of the derivative and proportional in series, especially if there is poor measurement resolution and no signal filter or derivative filter.
Most modern PID controllers use the ISA standard form, also known as the ideal form. The contribution from each of the modes is computed in parallel in the block diagram for the ISA standard form with a conventional integral mode. If the rate time is zero, the ISA standard form and the series form are effectively the same if the implementation of the integral mode is identical.
The ISA standard form eliminates interactions between the modes in the time domain leading to the name "non-interacting." Often not recognized are the interactions between the modes in the frequency domain of ISA standard form. The Laplace transform of the ISA standard and series algorithm reveals interaction and no interaction, respectively, between the terms. The label "non-interacting" is technically inappropriate in that while the ISA standard form is non-interacting in the time domain, this form is interacting in the frequency domain. Correspondingly, the series algorithm is interacting in the time domain, but non-interacting in the frequency domain. Both forms have a gain multiplier in the contribution from each mode, which is not the case for the parallel form.
In the parallel form, the contribution from each mode is computed in parallel. but the gain tuning setting only affects the proportional mode. The tuning setting for parallel integral and derivative modes are sometimes called integral and derivative gains rather than reset and rate times. Since there is no multiplication by the gain setting for the integral mode, the units of repeats per minute or seconds per repeat are meaningless. The units for integral and derivative gains may not even be given.
The parallel form is rarely used in industrial systems, but is commonly seen in control theory textbooks. Consequently the parallel form is mistakenly programmed into dynamic models for control studies and operator training systems, causing potentially disastrous results if tuning settings are moved from simulations to industrial systems, since the difference in integral and derivative settings can be quite dramatic. For PID controllers with high gain settings, the parallel form reset and rate tuning settings could be an order of magnitude or more larger than what can be used by an ISA standard form.
Greg McMillan
[email protected]
A: I believe the Z-N equations were developed originally based on the interacting form of the PID equation.
Rick Meeker
[email protected]
A: It is a simple question, but as far as I recall, it is not clear from the Z-N paper what controller (series or standard) was used by Ziegler and Nichols for deriving Z-N equations.
You may check:
Ziegler, J.G. and Nichols, N. B., "Optimum Settings for Automatic Controllers," Transactions of the ASME, Vol. 115, June 1993, pp. 220-222.
Ziegler, J.G. and Nichols, N.B., "Optimum Settings for Automatic Controllers," Transactions of the ASME, Vol. 66, Nov. 1962, p.759-768.
The good news: There is no difference for PI controller settings. For PID controllers, we may safely assume that at that time (1942), the PID controller was pneumatic/series, so formulas are for this controller structure.
Willy Wojsznis
[email protected]
A: J. G. Ziegler and N. B. Nichols were never concerned with the internal nature of the controller. They expected the settings, reset rate and proportional band to be independent of each other, that is, non-interactive.
The concept of interactive and non-interactive, to my memory, did not come into existence until the late 1970s. Perhaps it was a meaningless advertising gimmick, or born of ignorance of the work that had already been done in the field, or a "what if" plaything for academics. Perhaps it was a little bit of each.
At the time, it seemed that a three-adjustment controller was made into a five-adjustment controller with the derivative and integral adjustments having separate gains. It imparted no advantage and only added complexity and confusion to the optimum controller tuning issue experienced by the people at the process level.
To Ziegler and Nichols, as long as the dials indicated gain (dimensionless, or 100/proportional-band in %), reset (repeats of the proportional band per minute [others preferred the reset time in minutes]) and pre-act or rate action (derivative time in minutes), the device acted in conformance to the dial settings, and the settings were independent of each other, the controller was a controller by what ever name or technology employed. To them it was the controller designer's job to make sure that these performance characteristics remained unaltered as the design of controllers changed from pneumatic, to electronic, to digital and computer-based. They had done their work to be foremost of service to the people at the process level, and secondly to the designers of process control loops so that they could suggest start-up values for controller settings on the basis of the physical parameters of the process and the chosen valve and sensor ranges.
When you are faced with a PID controller that has more than three adjustments (and the adjustments are interactive) my recommendation is to consult the manufacturer's literature first, and failing to get satisfaction as to what to do, set all three gain adjustments to the same value as determined by the Z-N ultimate gain or reaction rate, root locus, frequency response or any other credible method that suggests starting values for each one of the three PID adjustments, and no more. Similarly, set the integral and derivative times to the values suggested by your favorite method.
In fine-tuning a process controller with more than three adjustments, keep the gains always in step, otherwise confusion will reign when the effects of changing the derivative and reset times are evaluated. An even better suggestion is to never use a PID controller, whatever its physical form, with more than three knobs, adjustments or program settings. You will be doing the people at the plant level a great favor.
Ziegler and Nichols did their seminal work while working for the Taylor Instrument Companies. I overlapped N.B. Nichols presence there as a researcher for ten years. We had many discussions on these topics as newer forms of controllers were offered to our customers.
Otto Muller-Girard, PE, FISA
[email protected]

Leaders relevant to this article: