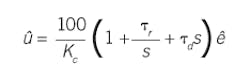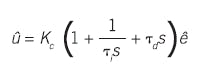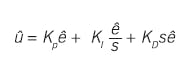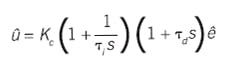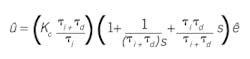Clarifying PID terminology confusion
This column is moderated by Béla Lipták, automation and safety consultant and editor of the Instrument and Automation Engineers' Handbook (IAEH). If you have an automation-related question for this column, write to [email protected].
Q: Mr. Liptak, I just read the excellent article entitled, “PID terminology causes confusion.” However, I'm still confused. In particular, Richard Caro says, “What Béla calls the 'independent' form of PID, I call 'traditional.' ” That seems to differ from the other answers. I tried to line up the terminology as follows:
- Standard = traditional = dependent
- Parallel = independent = non-interacting
Is that correct? Or do I have dependent and independent switched as Richard Caro would suggest?
Bob Jones, Senior Controls Engineer
[email protected]
www.integralconsulting.com
A: Yes, you're right. In 1942, when Ziegler and Nichols came up with their tuning method for the PID controller, they probably assumed it would not take 80 years to figure out what to call their basic equation and its variations. No such luck!
You're also right that pneumatic controllers are not independent. In pneumatic controllers, the three settings are physically interconnected, so if one is changed, it affects all the others. This does contribute to safety because this way the controller action will not reverse (and possibly cause accidents) when accidentally or through ignorance Td is set larger than Ti/4. In contrast, the non-interacting controllers need software protection to make sure that Td doesn't exceed Ti/4.
It would probably be best if, in cases where the gain of the PID acts on all parallel devices, calculated modes be called "standard.” I understand that ISA tends to agree with this view, but haven't formally acted on it. Similarly, it might be time to agree on terminology for the many other systems such as for multivariable, model predictive control (MPC) and artificial neural networks (ANN).
Béla Lipták
liptakbela @aol.com
A: I've formed an ISA 5.9 Committee to create a technical report on PID algorithms and performance. We're wrestling with these terminology problems, and decided to use “parallel” with the alternate name “independent” for the algorithm where the PID gain is only applied to the proportional mode. We're using the term “standard” also known as “ideal” for the algorithm where the PID gain affects all modes that are computed in parallel. We're using the term “series” also known as “real” for the algorithm where the derivative mode is computed first and is in series with the other modes. We're avoiding the terms "interacting" and "non-interacting" since what's interacting in time domain may be non-interacting in frequency domain.
The following ISA Mentor Program Q&A Blog addressed the conversion of settings:
https://automation.isa.org/how-do-you-convert-tuning-settings-of-an-independent-pid/
If you'd like to join the ISA 5.9 committee, let me know.
Greg McMillan
[email protected]
A: Your line-up of the terminologies is correct. The problem is that for many years manufacturers’ literature and even many textbooks were wrong in calling the PID implemented by pneumatic and even early electronic controllers “independent.” It was not! That format and the “standard” PID implemented by most digital controllers (DC) and single-loop controllers is the “dependent” form of the algorithm. I don’t know why they wrongly called it “independent," but perhaps the marketing teams just didn’t like to use the term “dependent.” It was also wrong to call this the “ISA Form of the PID.” There was never an ISA standard for the PID, and there is still no ISA standard for the PID algorithm.
Dick Caro
Certified Automation Professional (ISA)
[email protected]
https://dickcaro.blogspot.com/
A: Yes, it's confusing. Unfortunately, there are many names for the several key versions of the PID algorithm, and many of the names such as series or parallel are applied to two distinctly different PID formulations. I think it's best to identify the algorithm formulation by its calculus or Laplace representation to make clear distinctions.
A Laplace representation of the standard algorithm is:
This has been called "parallel" because the block diagram has the P, I and D operations in parallel. But it's also called "series" because in this mathematical form the controller gain multiplies each of the terms in series. It's called "ideal" because it's the form that arises from controller synthesis.
It's also been called the ISA standard, even though ISA has not declared it so. It's called "non-interacting" or "non-interactive" perhaps as a marketing trick to make it seem to be lacking some essential feature of the interacting controller. ISA has a committee 5.9 associated with standards, and is moving toward recommending the nomenclature that would label this form “standard,” but not declaring this as the right way to formulate the P, I, and D functions.
There are many versions of how this standard equation can be represented. If proportional band is used to represent the gain (PB = 100/KC) and reset rate is used instead of integral time (τr = 1/τi), then the equation appears as:
Although it appears different, there is no new functionality.
If the controller gain and actuating error are multiplied onto each term in the parenthesis, the standard form becomes:
Again, there is no alternate functionality, but this version has been given multiple names. "Independent gains" because of the three gains, and "parallel gains" or just "parallel" because of the structure. The ISA 5.9 committee is moving toward recommending the label "parallel."
The rate-before-reset version is:
This too can be mathematically factored in many ways. Here the term is 'leaded actuating error,' a projection of what the actuating error is anticipated to become. Then the P and I operations are on the anticipated error. In a block diagram this calculates the rate before the integral (often termed the "reset function"), hence the "rate-before-reset" name. But also, the block diagram suggests the name "series". It is alternately known as the "physically realizable controller" because this is how D was added to PI functionality in the initial mechanical-pneumatic device era. If you multiply the two binomials and collect common terms, then the Laplace formulation becomes:
This reveals the interaction of terms. If you adjust the derivative action, it also adjusts the P and I terms. So, it's often called the interacting or interactive version. "Interacting" as a controller description seems to convey a desirable feature, but I think the interaction is really a confounding attribute. ISA 5.9 is moving toward recommending the label "series."
The ISA 5.9 committee is in preliminary stages, and ISA has not yet declared any terminology as standard or even recommended.
Note that in spite of many versions, all have, and only have, the three functionalities of P, I, and D. One controller version is not functionally better than another. But there are many ways to present the controller terms. So for tuning, the user needs to know exactly how the vendor structured the algorithm.
There are many other embodiments for each of these three PID versions. These include velocity mode and reset feedback (a filter) to replace the integral. And a vendor can choose any of many numerical methods to digitally calculate the integral or the derivative, or initialize terms in MAN mode, or reset the integral when a constraint is encountered. So there are many more versions than just the basic three revealed above. A chapter in the Instrument Engineer’s Handbook provides additional information: Rhinehart, R.R., H.L. Wade and F.G. Shinskey, “Control Modes – PID Variations,” Instrument Engineers' Handbook, Vol II, Process Control and Analysis, 4th Edition, B. Liptak, editor, Section 2.3, pp. 124-129, Taylor and Francis, CRC Press, Boca Raton, Fla., 2005.
R. Russell Rhinehart
emeritus professor
School of Chemical Engineering
[email protected]
www.r3eda.com