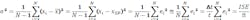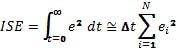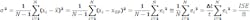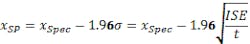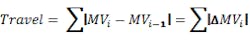My perspective on this question is from experience in the process industries where, characteristically, applications are nonlinear and relatively slow, and have a modest level of signal noise and substantial concerns related to safety.
Tuning is usually tested with setpoint changes (servo mode) using deviations from the new setpoint as the measure of goodness. And, usually, goodness of control is based on observing the controlled variable (CV) trend over time. If overshoot and undershoot (for example, too hot, too cold) material is blended downstream, then integral of the error (IE), where error is the controller actuating error or deviation from setpoint, could be an appropriate measure of control goodness.
In the IE method, plus and minus errors balance each other. However, if either deviation is bad, then integral of the absolute value of the error (IAE) could be the right measure. For example, the customer may like a bit of extra purity, but the manufacturer may not like the extra energy it takes to make the higher purity. Here, either deviation is undesired. But often, small deviations are inconsequential, and large ones are detectably bad. In this case, integral of the squared error (ISE) is appropriate.
Integral of time-scaled absolute error (ITAE) and integral of time-scaled squared error (ITSE) penalize persisting oscillations (or any sort of deviation) from setpoint by multiplying the actuating error by the time-since-the-setpoint-change. These metrics would seek to improve settling time in servo mode.
All of those measures quantify the impact of deviations from setpoint. But an older, still popular, criterion is damping rate, with quarter-amplitude damped (QAD) the custom. In QAD, the controller is tuned so the second overshoot is ¼ of the first. The overshoot is the beyond-shoot. It could be either above or below the setpoint depending on the direction of the activating setpoint change. The overshoot is in the same direction as the setpoint change.
Although we use the term “integral,” the actual metric is calculated numerically from sampled data, not continuum values, and over a finite time period, not for infinite time. Here is a nominal definition for ISE, and its calculation using the rectangle rule of integration:
ISE is my favorite of all of these sorts of measures of CV response because, when normalized by time, it represents the process variance during regulatory periods. Most of the time, processes are not being changed, but they are being regulated—they're being kept at the same setpoint. Process variance, which determines how close the setpoint can be to product specifications, would be an excellent choice for assessing control goodness. This expansion shows the relation to σ and ISE normalized by collection time, t:
If the product specification is x ≤ xspec, the CV standard deviation is σ, and the desire is to only violate the specification 95% of the time, then the setpoint needs to be:
But, in this regulatory case, testing goodness of controller tuning would not be in response to setpoint changes. To test in the regulatory situation, choose the controller coefficient values and collect data in an extended regulatory period, long enough to experience the control response to the range of vagaries that the process might experience.
Although ISE is my default choice, a particular application situation may make one of the other metrics (IE, IAE, ITSE, QAD, etc.) more appropriate. Understand your process and its context, then choose a right CV metric.
Goodness of control should also consider the impact on the manipulated variable (MV), the controller output. In my opinion, exclusively using the metrics of CV performance to tune a controller often result in a controller that aggressively moves the valves. This undesirably and excessively upsets utility streams, stresses equipment and propagates upsets downstream. One measure of MV action is energy, which is the sum of squared incremental changes in the MV at each sampling. Another is travel, which is the absolute value of the incremental MV changes since the last adjustment.
If the MV needs to change from 50% to 60%, but does it by jumping to 80%, then 55%, then 75%, then settling at 60%, it has traveled 95% just to make the 10% change.
I think that CV criteria for tuning often overlook the impact on the MV. The CV tuning criteria lead to aggressive controllers. However, because of safety, propagation of upsets in utility lines, thermal stresses, operator response to oscillating conditions and robustness to process gain changes, operators usually prefer controllers to be more temperate, and move the process in a fast-enough but over-damped manner.
Although CV and MV issues are important, I think that three items related to controller tuning have an even stronger claim in evaluating tuning:
1. Operator/technician/engineer time/skill is the most important criteria. A tuning procedure should be fast, robust, and simple (no complicated calculations).
2. A tuning procedure should not be invasive. It should not upset the process. This is the second most important criteria.
3. Tuning must accommodate what the controller might encounter, not just what the process is at the instant it is being tuned. Processes are nonlinear, which means the gain, time constants and delays are not constant, but depend on operating conditions, which continually change. A tuning procedure should permit the tuner to balance CV and MV issues in the situation context over the likely future conditions.
If I wrote a textbook on process control, I would include many of the standard tuning approaches (ZN Ultimate, lambda, controller synthesis, FOPDT model-based, Cohen-Coon, ATV, etc.). They have value in revealing analysis of dynamic systems and the historical context of the profession. But I don’t use them. They take too long, induce process upsets that are too large for comfort, presume the controller coefficient settings are properly calibrated, require calculations, use the too-aggressive CV measures, and presume that the process is linear.
I use and teach a heuristic approach to tuning. It's based on the standard PID algorithm:
1. Adjust the gain in a P-only controller until there are about three detectible movement directions in response to a modest setpoint change. Make sequential setpoint changes in up-down-down-up pattern to minimize process deviation from the nominal value. Start with a low Kc value to minimize tuning-induced upsets. Double or halve the Kc value if searching; then when the range is identified, interval halve to fine tune. There is no need to get exactly three wiggles—2.5 or 3.5 is fine. It may be easier to see the signal wiggles in the MV than in the CV. If there are more wiggles on one side than the other, use the more aggressive side.
2. Set the integral time to half of the period of the oscillations.
[sidebar id =1]
3. In the rare case that derivative action is desired, accept the norm of the conventional tuning rules, and set the derivative time to ¼ of the integral time.
4. Set options that you would like (such as P-on-x, velocity mode, anti-windup).
5. Fine tune the PI or PID controller gain by testing with setpoint step changes over the operating range desired. Avoid oscillatory action. Accept sluggish control in one direction or one operating region, if it prevents oscillatory action in another region that might be encountered.
This heuristic approach is fast, confidently done, has small impact on the processes, and includes human supervision. I suggest that you rise above any theory you may have been taught about one aspect of tuning, and practice heuristic tuning with a comprehensive set of evaluation criteria.
[sidebar id =2]
