Model-less multivariable control in practice

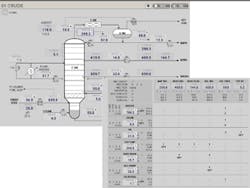
Figure 1: Similar to model predictive control (MPC), model-free control (XMC) matrix rows are the direct control variables (DCVs), whose setpoints or outputs are directly adjusted by the multivariable controller, while the columns are the indirect control variables (ICVs) that are indirectly controlled by the DCVs

A core concept carried forward in model-less technology is the matrix, which is the natural way to illustrate the multivariable nature of processes and to frame the multivariable control problem, regardless of models. Figure 1 is the matrix for a simulated crude oil distillation unit XMC application. The matrix rows are the direct control variables (DCVs), i.e. variables whose setpoints or outputs are directly adjusted by the multivariable controller (similar to MPC manipulated variables). The matrix columns are the indirect control variables (ICVs), i.e. variables that are indirectly controlled by means of the DCVs (similar to MPC controlled variables). Some commercial products reverse the rows and columns, which is arbitrary (and bothersome).

The biggest hurdle to understanding model-less control is often overcoming the past paradigm that model-based control is the only way the problem can be solved. As we saw in Part 1, manual multivariable control has always been an essential aspect of nearly all industrial process operation, even before computers. Model-less multivariable control concepts borrow heavily from historical manual methods, while meeting the overall design criteria shown in Table I (explained further in Part 1).

Constraint control and optimization

One of the first questions often asked about model-less technology is: how does it control? After which, the next questions is: but surely it can't do optimization?

These questions can be broken down further: how are constraint control moves arrived at? What control technique is used to arrive at appropriate move rates and to approach constraint limits and targets without overshoot or cycling? And, how are optimization moves determined?

The technical answers to these questions are: a logic-based directional move solver; pre-selected DCV move rates combined with rate-based control (RBC); and pre-assigned operator-adjustable optimization targets. However, it also helps to consider how manual, multivariable control has been carried out in the past, and still is today.

In industrial process operation, the operating team is always well aware of the key process interactions, constraint limits and optimization targets that form the basis of multivariable constraint control and optimization. A system of logic is sufficient to capture this knowledge, and arrive at the correct DCV move directions under various process circumstances, just as members of the operating team would do mentally, before implementing the moves manually.

In model-less technology, DCV move rates are preselected, which is not only easier and more reliable than calculating them dynamically, but it's also more appropriate to select move rates during the controller design meeting, based on experience, procedures, safety and stability. This also reflects historical manual methods, where established reasonable move sizes are usually well known within operations, if not explicitly given in procedures.

Finally, RBC is used to taper the DCV move sequences in a manner that lands ICVs on the constraint limits and optimization targets without overshoot or cycling, which is a more realistic and relevant performance criteria than "error minimization." In this respect as well, RBC reflects sensible historical manual methods, whereby operating team members know approximate process response times, and reduce or cease moves ahead of time in order to approach limits or targets in a ramp or first-order fashion.

MPC engineers, who usually know model-based technology relatively well but often understand the nature of industrial process operation more superficially, are often surprised that the real-world multivariable control problem can be solved in this straightforward manner, hence the questions. Operating team members, on the other hand, are often surprised to realize that MPC employs such elaborate measures to reach conclusions that they consider to be intuitively obvious. While model-based technology is theoretically sound and even elegant, it's often basically overkill and simply unnecessary for the control purposes normally at hand, in addition to its vulnerabilities in practice as mentioned in Part 1.

RBC automates intuition

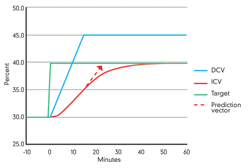
RBC (patent pending) is a reliable, adaptive and predictive method to control ICVs to constraint limits and optimization targets without overshoot or cycling, in a manner consistent with desired industrial operational performance. RBC works in conjunction with the directional move solver. The directional move solver determines the moves that are indicated based on current values (typically every 5 seconds), and RBC may then taper or cancel some of those moves based on the ongoing approach rate of ICVs to their constraint limits or targets. Figure 2 illustrates the basic control mechanism of RBC, which derives from the fundamental mathematics and dynamics of first order systems.

Figure 2: At time zero, the indirect control variable (ICV) target value increases. The gain direction is positive, so the direct control variable (DCV) must increase to move the ICV to the increased target. Under rate-based control (RBC), DCV begins increasing at the preselected move rate. When the rate of change of the ICV indicates it will reach the new target within one time constant (10 minutes in this example), DCV moves are halted, which results in the ICV ultimately landing exactly on the new target value, in a first-order fashion (three time constants later).

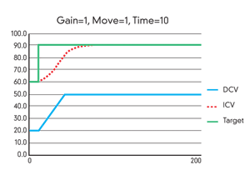
RBC is inherently adaptive to changes in process gain, which has been a particular vulnerability of model-based methods. For example, as shown in Figure 3, if the process gain doubles, the ICV will increase at a faster rate, and the DCV moves will be halted correspondingly sooner, so that the ICV once again ultimately lands exactly on its target (thereby giving industry perhaps its first truly inherently adaptive control algorithm).

Figure 3: Rate-based control (RBC) is inherently adaptive to changes in process gain and move rate: if the process gain doubles, the independent control variable (ICV) will increase at a faster rate, and the dependent control variable (DCV) moves will be halted correspondingly sooner, so the ICV once again ultimately lands exactly on its target.

By a similar analysis, RBC is adaptive to changes in the pre-selected move rate. This has important advantages because it allows move rate, which is an operational performance tuning parameter, to be changed without affecting control performance. It also allows the move rate to be tailored and dynamically adjusted, for example, to use a slower optimization speed or a faster critical ICV response (Figure 3).

RBC is also predictive, in that the current ICV rate of change is used to predict the future value and take appropriate control action. This is a much simpler concept of "predictive" than the model-based concept, yet for practical purposes it can be more reliable. For example, when approaching a stop sign in a car, would you rather use current speed to judge when to apply the brakes, or acceleration history and multiple unsure models?

RBC control performance is "robust" (i.e. relatively insensitive) to changes in process response time. Approximate response time, like move rate, is usually well-known among the operating team, and can be confirmed using historical process data. If actual process response time varies by half or doubles, the effect on RBC control performance is very modest (also shown in Figure 3). Suggested practice is to use response times slightly conservatively at 1.0-1.5 times the normal process response time (or, technically, the process response first order time constant).

How model-less does feedforward

Model-less technology is a method of accomplishing multivariable constraint control and optimization without the use of models, but it does not disregard or preclude the use of feedforward models where necessary. In process control practice in general, feedforward can be one of the most effective techniques to reject process disturbances seamlessly by acting on measured disturbances before they impact the process, especially in the case of slow or dead-time-dominant dynamics. But successful feedforward control requires very robust models.

Feedforward model-based predictive control (essentially redundant terminology), like multivariable control itself, has been around since long before computers2. Nearly every industrial single-loop controller, whether a piece of standalone hardware or a DCS function block, has provision for feedforward inputs. Despite the potential power and availability of feedforward functionality, it's always been used sparingly because, unless the model is highly reliable, it can easily do more harm than good. For reliable advanced control performance, each feedforward model should be reliable and sufficiently beneficial to justify the effort and risk of using it.

That's the traditional advanced regulatory control (ARC) philosophy relative to feedforward and (in the author's view) the wholesale manner in which MPC employs feedforward and its ensuing performance and maintenance track record have largely validated this wisdom. In model-less practice, feedforward models are normally used on a selective basis, with applications typically involving only a handful of rudimentary models at most, or often none at all, depending on actual application needs.

In XMC, feedforward is normally incorporated in the form of predictive ICVs, i.e. feedforward information is built into calculated ICV values using traditional ARC techniques. Where a reliable model is not possible (usually due to process complexity) or the ICV is not critical (such that it does not warrant the effort or risk of a model) XMC also includes a basic dead-time control algorithm. No feedforward is necessary for the majority of first-order, relatively fast ICVs.

Scales well to small matrices

There's no reason that model-less technology can't be combined with big-matrix practice, but philosophically, model-less technology goes hand in hand with small-matrix practice.

Industry-standard "big-matrix" practice involves drawing an envelope around the process, identifying all the process interactions within, and including all or most of the resulting models and variables in the matrix design. The unpredictability of a large matrix with dozens of variables and often hundreds of models has frequently resulted in both incorrect and unwanted control action, leading to well-known, non-best operating practices, such as detuning and clamping. MPC engineers have instinctively pruned matrix designs over the years, but the sensible bottom to this trend is to include only the relative handful of variables and models that are already proven to be important and reliable in prior manual operation, i.e. "small matrix" practice.

Another way to view the difference is that big-matrix practice involves applying a more operationally abstract technology that in theory will do more complete job of finding the "true" constraint control and optimization answers. Meanwhile, small-matrix practice builds a compact matrix design, purpose-built to mimic existing operational criteria and methods.

Costs vs benefits

Model-less technology has the potential to reduce the cost of ownership of multivariable control by an order of magnitude, while preserving or even increasing benefits. Other important benefits include agility (ease of deployment and modification) and scalability. Low cost and ease of deployment mean that model-less technology can capture smaller applications that in the past could not be considered due to the high cost and resource intensity of model-based tools.

By eliminating models, ownership costs are reduced at every lifecycle stage, including procurement, design, deployment, training, operation, maintenance, modification and performance monitoring. Model-less technology also has the potential to move multivariable control from the domain of specialists into the domain of a routine operational competency, such that design, deployment and operation can be accomplished by the operating team and in-house control engineers, using existing DCS control system capabilities. This is a potentially critical consideration going forward, because nearly all processes are multivariable, meaning successful process operation demands a degree of in-house multivariable control competency and agility that has largely failed to materialize under MPC.

Model-less technology basically does the same job as model-based technology, so while costs are lowered, economic payback benefits remain comparable or potentially increase due to potentially increased effectiveness plus the prospect of capturing more small and mid-sized applications.

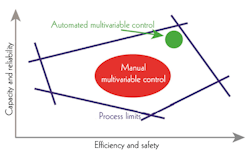
Figure 4: This classic "constraint corner" diagram shows how multivariable constraint control and optimization allow the process to run at higher capacity, reliability, efficiency and/or safety.

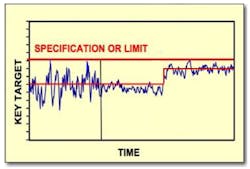
The lion's share of traditional multivariable control benefits come from consistently "pushing" constraint limits and optimization targets as the process operating point moves within the overall operating window due to disturbances in feedstock quality, feed rates, ambient conditions, equipment performance, product specifications, optimization targets, etc. This is the classic "constraint corner" concept as shown in Figure 4. A second category of traditional benefits is "path optimization" (a.k.a. error minimization), which refers to minimizing the integral of error as the process is moved from current conditions to optimum conditions. And a third category of traditional multivariable control benefits is process variance reduction, which then allows the process to be reliably operated closer to the constraints, thereby incrementally increasing earnings, yield, energy savings, etc. Figure 5 shows this classic concept.

Figure 5: Multivariable constraint control and optimization allows processes to run closer to constraints by reducing variance.

XMC performs well in all these areas. In practice, neither the potential of models nor the limitations of model-less hold completely true, so that overall performance and benefits become comparable. In initial field tests, operators and engineers like the simplicity, reliability and responsiveness of XMC. Table II compares returns on investment for large- and small-matrix projects using model-based and model-less methods.

References

1. "Online monitoring of multivariable control utilization and benefits," A. G. Kern, Hydrocarbon Processing, October 2005.
2. "Process modeling, feedback controllers," Jim Ford and Bruce Brandt, Consulting-Specifying Engineer, July 2015.
3. "Multivariable control performance: the case for model-less," by A. G. Kern, InTech, July-August 2014.
4. "Small-matrix, model-less multivariable control," A.G. Kern, Chemical Engineering, February 2014.