Validating and using linguistic cause-and-effect rules
Operators have a great deal of process experience, and they use it to anticipate upcoming outcomes that will require action. They observe events happening and anticipate what they mean. For example, they anticipate there will be excessive waste, needs to clean equipment, constraints on throughput, etc. Then, they take a control action justified by what their experience indicates they should expect. Maybe that action is to temporarily divert the product to intermediate inventory for quality checking, or shift a temperature setpoint to accommodate the situation.
Similarly, managers have experience and qualitative rules about how their manufacturing and human processes behave. They make decisions based on those rules.
A human linguistic rule has an antecedent and a consequent:
IF [antecedent] THEN [consequent]
For example, as a simple rule, we have family in Nashville, Tenn., and have observed that if it rains in Stillwater, Okla., it will rain in Nashville about one day later. Or if it's hot in Stillwater, then in a day, it will be hot Nashville.
IF [T in Stillwater is Hot] THEN [T in Nashville will be hot AND there will be a delay of one day]
This doesn't mean the weather in Stillwater is the reason for the weather in Nashville. They're both effects of the same cause, a weather pattern that moves toward the east. But we can observe the weather today in one place, and tell our friends to prepare for what tomorrow brings in another. And they can take appropriate action or make appropriate plans.
Rule forms and data-based testing
Operators and managers may have developed cause-and-effect conclusions about their process. The antecedent may have AND, OR or NOT conjunctions. Generically, a linguistic logic rule might be:
IF [(x is A) AND ((y is B) OR (z is C))] THEN (w is D) AND (t is T)]
Here x, y, z, w and t are variables, and A, B, C, D and T are linguistic categories or classifications. The representation (x is A) may mean the process temperature (x) is in the category called “hot” (A). Meanwhile, (y is B) may mean the raw material source (y) is from the recycle bin (B). Then, (t is T) may mean the delay (t) is short (T). Using fuzzy logic concepts, each element in the antecedent has a membership function, and the value of the variable has an associated belongingness to the linguistic category, µA(x), µB(y), etc. Belongingness (µ) is the value of the membership function, which has a value from 0 (no belongingness) to 1 (a perfect fit). Then, (x) and (y) are variables, and A and B are the categories. For example, the temperature during the summer of 2022 was relatively hot, µRelatively Hot(Summmer 2022 Temperature) = 0.9. You may have experienced something other than I did and categorize it as 100% relatively hot, µHot(T)=1, or not unusually hot, µHot(T)=0.8.
I wrote about fuzzy logic and natural language processing in two Control articles: “Automating human reasoning with natural language processing, Part I” in March 2021. Part II appeared in April 2021.
Similar to logic gates, the OR conjunction might take the maximum of the two belongingness values. Then, in the third equation the TRUTH of [(y is B) OR (z is C)] might be MAX{µB(y), µC(z)}. The TRUTH of the AND conjunction might be the minimum of the two belongingness values. Then the TRUTH of the antecedent in the third equation would be MIN[ µA(x),MAX{µB(y), µC(z)}]. The TRUTH of the consequent is MIN[µD(w), µT(t)].
Alternately, some use the membership functions as if they were probabilities, and the TRUTH of an AND is the product, µD(w)⋅µT(t), and the TRUTH of an OR is the complement of the product of the complementary values, {1-[1-µB(y)]⋅[1- µC(z)]}. A problem with this approach is that when there are many items in the term, the product seems to exaggerate the values. For instance, if both are 0.8 the AND product TRUTH is 0.64 and the OR TRUTH value is 0.96. I prefer a geometric mean. With this, the AND TRUTH is [ ∏nµLC (x) ]1/n, and the OR TRUTH is {1-[ ∏n(1-µLC (x))]1/n}.
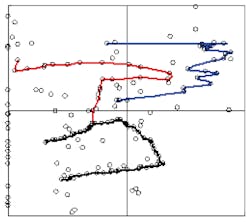
As continuous process variables evolve over time, the process state will not jump to unconnected spots, but will progressively indicate a time-path locus through the TSD, as illustrated by the blue, black and red connect-the-dot traces in Figure 1.
However, if the process is infrequently observed, has a large delay, or is an end-of-batch result, the data set is independent from the prior value and markers may jump to new places without tracing a path.
Data in Q-I affirm the rule.
Data in Q-IV indicate that the rule is wrong. It could be because the cause-and-effect concept is not true. For example, one of my grandmother’s rules was: “IF you sweeten your tea, THEN you will get diabetes.” Alternately, the rule could be partially right with an erroneous OR conjunction. For example, “IF you stub your toe OR it rained last week THEN your foot will be in pain.” The weather last week is mechanistically irrelevant. Every time it rains, if you don’t stub your toe, the marker will be in Q-IV.
Data in Q-II also indicate that the rule is wrong, but it could be partially true and just over-specified. For example, “IF it does not rain for three months AND you have 43 letters in your city name THEN there will be a drought.” The city name is mechanistically irrelevant, so the AND conjunction is irrelevant.
Data in Q-III provide neither affirmation nor rejection of a rule. As described by the rule, neither the consequent nor the antecedent happened. But this doesn't mean that the event of concern didn't happen. If the event of concern did happen, then the rule-stated antecedent and/or consequent are an erroneous description.
The blue trace in Figure 1 shows a time-based sequence from continuous process data. It suggests that the rule is substantially valid, but with only 75% truth of the consequent and a few points in Q-II. Data also indicates that the rule or the linguistic classification breakpoints might be fine-tuned.
The black trace in Q-III of Figure 1 indicates that the rule was mostly not active—neither the antecedent nor consequent meaningfully happen. But when the antecedent is activated, the black trace in Q-IV indicates that the rule isn't true or that it's incomplete, needing another antecedent AND condition or removal of an antecedent OR condition.
The red trace in Figure 1 suggests that the rule is somewhat true (Q-I data) but also over-specified (Q-II data). The rule is promising but not quite right.
Data marginally in a quadrant would moderately suggest affirmation or rejection, and should cause fine tuning of the rule. Data in both Q-I and either Q-II or Q-IV indicate the rule is true sometimes but not always, and should cause fine tuning of the rule.
The figure uses the 0.5 antecedent and consequent truth boundary values to define Q-I. Our research suggests that the 0.75 values are better for definitive affirmation judgments about a rule.
Using the TSD to select rules
There may be competing rules about how to forecast what will happen—Jim’s and Bill’s rules, for instance—and it would be good to have data to settle the argument. Sue may have an almost good rule, but data may indicate that it's missing some antecedent condition. Ted may have a bad rule that needs to be discarded, and Ted needs to see evidence that he can accept. We could plot such rule goodness metrics in the TSD to see how valid the rule is, and use this to help direct rule improvements and better understand the cause-and-effect relations, which will permit us to better manage the processes.
The processes may be human: if the kid doesn't go to bed on time, he’ll be grumpy, whiny and disagreeable the next day. If students are forced to have 7:30 a.m. or Saturday classes, they’ll skip many and end-of-course assessment of education quality will be low. If a manager plans 4:30 p.m. meetings, employee morale will be low.
I believe that linguistic rules, which embody human interpretation of observed experience, when validated by data, can be trustworthy as information to guide decisions related to managing those processes.
A benefit of such human linguistic rules over those developed by statistical data processing (such as machine learning) is “explainability.” The human logic has a mechanistic, cause-and-effect relationship. If data affirms the rule, then the logic is also affirmed, and the relation can be explained.
Research findings
The Measurement and Control Engineering Consortium, made up of the NSF and about a dozen company sponsors at Oklahoma State University and the University of Tennessee, had several projects related to this modeling concept for chemical processes. It took several approaches to develop the rules.
One was to set a rule structure and then enumerate all possible rule conditions. From there, test each rule with the TSD on process data. This worked pleasingly for rejecting bad rules and accepting a set of good rules. But it required the human to create the original rule structure.
Once there was a subset of reasonably satisfactory rules, any sort of optimization to adjust the membership function breakpoints to improve the rule could be used. The rules were consistent with qualitative outcomes that were predicted by first-principles models and logical understanding of the processes.
However, one problem was that the human had to set a structure, so they looked at genetic algorithms (a form of AI) to generate rules using the TSD metrics as the objective function. This found some of the rules related to the process, but the procedure also missed some valid rules. Also, it generated some trivial rules, “IF (T is High) THEN (T is High)”, which are very true, but of no utility.
Another problem is the huge number of rules needed to completely describe a process. If there were two antecedent inputs with three linguistic categories each, and one consequent with three categories, there are 3 ^ 3 = 27 possible rules. For greater precision, maybe five linguistic categories, and if delays are included (a fourth variable), then enumerating one would get 5 ^ 4 = 625 rules. This is still a relatively simple process model.
The consortium concluded that using first-principles modeling was better (faster, more precise, revealing mechanisms) when you can understand processes. I also have chapters in my nonlinear regression modeling and statistics books for both logical- and data-based model validation. However, the fuzzy structure in antecedent and consequent, which embodies human understanding, works when the process is poorly understood. The TSD approach seems especially useful to test and select valid human linguistic rules from oral traditions and residual folklore, especially those used by operators and managers to take action.
Maybe one day AI will work in autonomous rule discovery. But rather than relying on AI to find the rules, I’d start with testing rules that humans already have. If they have a rule, it's about something important enough to have a rule for. If a rule is judged to be valid, TSD metrics would affirm some human intuitive cause-and-effect concept, and the system would have data-validation to justify passing the rule to others.
It could be, if a human defines the inputs thought to be important to an outcome, then classical empirical correlation modeling could discover the relations. But I like the “explainability” associated with linguistic mechanistic rules.
Keep accumulating data, for either of two reasons:
- Processes change in time. Piping reconfigures flow patterns, the new generation of employees has patterns that are different from older generations, etc. Rules that were once true may need to be adjusted as time progresses.
- Initial data in Q-I would indicate that the rule is true, but subsequent markers in Q-II or Q-IV would reveal that it needs some correction.
About the Author
R. Russell Rhinehart
Columnist
Russ Rhinehart started his career in the process industry. After 13 years and rising to engineering supervision, he transitioned to a 31-year academic career. Now “retired," he returns to coaching professionals through books, articles, short courses, and postings to his website at www.r3eda.com.

Leaders relevant to this article: