Open Loop Tuning and Process Control en Español
“Ask the Experts” is moderated by Béla Lipták ([email protected]), editor of the Instrument Engineer’s Handbook. In this column, he and other experienced process control engineers welcome questions concerning process measurement, control and optimization. If you want to ask a process-control related question, please include a sketch or a P&ID.
Q:I have come across your articles on process control and instrumentation and find them very good reading material. The discussion given in the following link is information about the implementation of cascade control in a process system. I have a question about the information presented in Figure 2 of your February 2006, column. (Cascade control tuning). This is a case of applying the open-loop test Ziegler-Nichols (ZN) method. Should the value of A be the same as K? In that case, the value of time constant T will be greater than 5 minutes (about 7.5 min)? I would like to assign this example as a case study of ZN methods for my class, “Fundamentals of Automation and Control.” I would appreciate if you could clarify this issue.
Weining Feng, Ph.D.
Associate Professor, Engineering Technology
University of Houston-Downtown
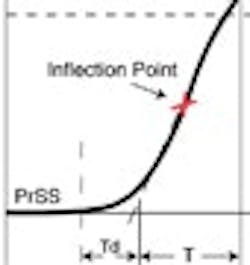
A:In the case illustrated by this Figure (see below), the distance A is smaller than K (the final value of the process variable after a step change in the manipulated variable. The distance A is determined as the point where the tangent through the inflection point of the reaction curve and the vertical line drawn at the end of the time constant T cross. Naturally, the reaction curve shown isn’t the only one possible. Different processes have different dynamics and, therefore, different reaction curves. As the process gain rises, the reaction rate (and the value of “A”) also increases. The settling time of processes also vary, and the longer the settling time (in multiples of the time constant T) the larger K tends to be.
The only case I can think of when A will equal K is a pure dead-time process with a time constant (T) of zero and a process gain of infinity. Fortunately, we don’t have such processes, though an explosion might come close to it.
BÉla LiptÁk
[email protected]
Open Loop Test for Non-Interacting PID Tuning
Figure 1. The distance A is the point where the tangent through the inflection point of the reaction curve and the vertical line drawn at the end of the time constant T cross.
There are several different versions of the Z-N open-loop tuning equations. The one I use calculates controller gain, rather than proportional band:A:
Kc = (0.83 T) / (Kp Td) = (0.83 T DeltaM) / (K Td), since Kp = K / DeltaM, using symbols from Figure 2. (Some publications use the figure 0.9 instead of 0.83 in the above equations.)
This equation can be converted to calculate Prop Band (PB), since PB = 100 / Kc.
Hence, PB = (100 K Td) / (0.83 T DeltaM) = (120 K Td) / (T ∆M).
Using data from the figure:
PB = (120 * 14 * 2.5 ) / ( 5 * 3) = 280%.
The equivalent gain is
Kc = (0.83 * 5 * 3) / (14 * 2.5) = 0.36.
I believe there are two errors in the equation in Figure 2 which calculated %PB.
- The constant 83 is used. I think this should be 100/0.83, or 120.
- The value of A is used. I think this should be K, not A.
Incidentally, to the best of my knowledge, few commercial controllers are tuned in terms of Proportional Band. (Many years ago, most of them were.) Today, most are tuned in terms of controller gain, rather than PB. I would recommend teaching students to use controller gain, rather than PB, but I would call their attention to PB and the conversion equations from one to the other.
Harold Wade
Wade Associates
[email protected]
A:The subject matter finds its roots in the 1942 Transactions of the ASME article, “Optimum Settings for Automatic Controllers” by N.B. Nichols and J.G. Ziegler of the then Taylor Instrument Company. Also referred to as the open-loop tuning method, it’s particularly applicable to processes with some self-regulation and sufficiently tolerant for operating away from the desired value during the period of open-loop upset to acquire the reaction graph and also to record the upset.
Four pieces of data are required:
- The percent of span magnitude of the step upset, Am, in Figure 2 of the inquiry.
- The ultimate size of the response, preferably also in percent of span, to the upset, K .
- The slope of the response curve at its steepest, i.e. inflection point. That slope, or tangent line, is to be expressed in percent of span of controlled variable (or response to upset) per unit of time, time units matching the controller calibration, usually in minutes. Any right triangle derived from the slope line will do. In the figure shown, a 0.63*K line has been introduced. Its intersection with the reaction response curve defines the value T. The vertical line through the T value intersects the tangent line at amplitude A. Value A divided by T is the maximum slope of the reaction curve. It’s what Ziegler and Nichols called the reaction rate, Rr, in the figure. While T, as defined here by taking 63% of the ultimate response, is on other occasions called the principle time constant of the process, this fact has no bearing on the controller tuning by this method. It’s simply a factor in the ratio: A/T = Slope = Rr. If K was taken as the amplitude, the corresponding value of t would have been t = T * K/A. The result in the sample computation, and hence the controller tuning, would have been the same.
- Lastly, the dead time, Td, the time between the start of the step upset and the intersection of the tangent line and the line representing the pre-disturbance quiescent condition, also preferably expressed in minutes.
The factor 83 in the example is empirical. Ziegler and Nichols recommended values in the range of 50 to 83 depending on the nature of the process and desired control responsiveness.
To answer the question then: A is not the same as K in the illustration. Rather, A is the result of the construction sequence that starts with the line at 0.63*K, the line through the intersection with the response curve, the vertical line defining T and, finally, the intersection of that line with the tangent line, thus defining A.
Otto Muller-Girard, PE,
ISA Fellow
Q:One of our readers asked about good books about instrumentation and process control in Spanish. Here are some recommendations from our panel.
A:Traditional automatic control books are all in Spanish. Among these are works by Ogata, Kuo, Dorf and Bishop. Books on process control available in Spanish include those by F.G. Shinskey and Smith & Corripio, but for instrumentation, I just remember the Spanish Book by Antonio Creus Solé called Instrumentación Industrial.
Dr. Rubén Darío Rojas Sulbarán
Coordinador Postgrado en Ingeniería Biomédica
Universidad de Los Andes, Facultad de Ingeniería
Mérida, Venezuela
A:One of my books, Nuevo Manual Sobre el Control de Procesos, is translated in Spanish. For more information about it, see www.topcontrol.com/techinfo/manuals9.php.
Michel Ruel, PE
President, Top Control
www.topcontrol.com
A: My Process Control Systems, 3rd ed., is published as Sistemas de Control de Procesos (1996), in two volumes, by McGraw-Hill in Mexico.
F. G. Shinskey
Process Control Consultant
North Sandwich, N.H.03259
A: My book, Foundation Fieldbus, has been translated to Spanish and Portuguese, thanks to Augusto Periera. It is available from ISA District 4.
Ian Verhappen, PE
Syncrude Canada
A: The Instrument Engineer’s Handbook has not yet been translated into Spanish, but if a publisher is interested in translating it or any of my other books, the English language publisher (CRC) would be glad to consider that.
BÉla LiptÁk
[email protected]