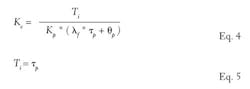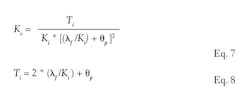By Greg McMillan, Sridhar Dasani and Dr. Prakash Jagadeesan
The tuning of level controllers can be challenging because of the extreme variation in the process dynamics and tuning settings. Control systems studies have shown that the most frequent root cause of unacceptable variability in the process is a poorly tuned level controller. The most common tuning mistake is a reset time (integral time) and gain setting that are more than an order of magnitude too small.
In this article we first provide a fundamental understanding of how the speed and type of level responses varies with volume geometry, fluid density, level measurement span and flow measurement span for the general case of a vessel and the more specific case of a conical tank. Next we clarify how tuning settings change with level dynamics and loop objectives. Finally, we investigate the use of an adaptive controller for the conical tank in a university lab and discuss the opportunities for all types of level applications.
General Dynamics for Vessel Level
There have been a lot of good articles on level control dynamics and tuning requirements. However, there often are details missing on the effect of equipment design, process conditions, transmitter calibration and valve sizing that are important in the analysis and understanding. Here we offer a more complete view with derivations in Appendix A, available on the ControlGlobal website (www.controlglobal.com/1002_LevelAppA.html).
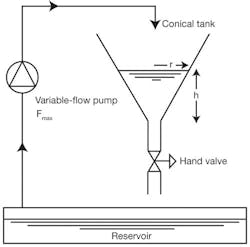
Figure 1. Conical Tank in MIT Anna University Lab with an industrial DCS.
Frequently, the flows are pumped out of a vessel. If we consider the changes in the static head at the pump suction to have a negligible effect on pump flow, the discharge flows are independent of level. A higher level does not force out more flow, and a lower level does not force out less flow. There is no process self-regulation, and the process has an integrating response. There is no steady state. Any unbalance in flows in and out causes the level to ramp. When the totals of the flows in and out are equal, the ramp stops. For a setpoint change, the manipulated flow must drive past the balance point for the level to reach the new setpoint. If we are manipulating the feed flow to the volume, the feed flow must be driven lower than the exit flow for a decrease in setpoint. The ramp rate can vary by six orders of magnitude from extremely slow rates (0.000001%/sec) to exceptionally fast rates (1%/sec). The ramp rate of level in percent per second for a 1% change in flow is the integrating process gain (%/sec/% = 1/sec). The integrating process gain (Ki) for this general case of level control, as derived in Appendix A, is:
Since the PID algorithm in nearly all industrial control systems works on input and output signals in percent, the tuning settings depend upon maximums. The flow maximum (Fmax) and level maximum (Lmax) in Equation 1 must be in consistent engineering units (e.g. meters for level and kg/sec for flow). The maximums are the measurement spans for level and flow ranges that start at zero. Most of the published information on process gains does not take into account the effect of measurement scales and valve capacities. The equation for the integrating process gain assumes that there is a linear relationship between the controller output and feed flow that can be achieved by a cascade of level to flow control or a linear installed flow characteristic. If the controller output goes directly to position a nonlinear valve, the equation should be multiplied by the slope at the operating point on the installed characteristic plotted as percent maximum capacity (Fmax) versus percent stroke.
Normally, the denominator of the integrating process gain that is the product of the density (ρ), cross-sectional area (A) and level span (mass holdup in the control range) is so large compared to the flow rate that the rate of change of level is extremely slow. For horizontal tanks or drums and spheres, the cross-sectional area varies with level. In these vessels, the integrating process gain is lowest at the midpoint (e.g. 50% level) and highest at the operating constraints (e.g. low- and high-level alarm and trip points).
Most people in process automation realize that a controller gain increased beyond the point at which oscillations start can cause less decay (less damping) of the oscillation amplitude. If the controller gain is further increased, the oscillations will grow in amplitude (the loop becomes unstable). Consequently, an oscillatory response is addressed by decreasing the controller gain. What most don’t realize is that the opposite correction is more likely needed for integrating processes. Most level loops are tuned with a gain below a lower gain limit. We are familiar with the upper gain limit that causes relatively fast oscillations growing in amplitude. We are not so cognizant of the oscillations with a slow period and slow decay caused by too low of a controller gain. The period and decay gets slower as the controller gain is decreased. In other words, if the user sees these oscillations and thinks they are due to too high a controller gain, he or she may decrease the controller gain, making the oscillations worse (more persistent). In the section on controller tuning, we will see that the product of the controller gain and reset time must be greater than a limit determined by the process gain to prevent these slow oscillations.
Figure 2. Conical tank detail.
In some applications, exceptionally tight level control, through enforcement of a residence time or a material balance for a unit operation, is needed for best product quality. The quantity and quality of product for continuous reactors and crystallizers depend on residence times. For fed-batch operations, there may be an optimum batch level. The variability in column temperature that is an inference of product concentration in a direct material balance control scheme depends on the tightness of the overhead receiver level control. Since these overhead receivers are often horizontal tanks, a small change in level can represent a huge change in inventory and manipulated reflux flow.
Figure 3. Performance of linear PID level controller for a conical tank.
In other applications, level control can be challenging due to shrink and swell (e.g. boiler drums and column sumps) or because of the need for the level to float to avoid upsetting the feed to downstream units (e.g. surge tanks). If the level controller gain is decreased to reduce the reaction to inverse response from shrink and swell or to allow the level to float within alarm limits, the reset time must be increased to prevent slow oscillations.
Adaptive level controllers can not only account for the effect of vessel geometry, but also deal with the changes in process gain from changes in fluid density and nonlinear valves. Even if these nonlinearities are not significant, the adaptive level control with proper tuning rules removes the confusion of the allowable gain window, and prevents the situation of level loops being tuned with not enough gain and too much reset action.
Specific Dynamics for Conical Tank Level
Conical tanks with gravity discharge flow are used as an inexpensive way to feed slurries and solids such as lime, bark and coal to unit operations. The conical shape prevents the accumulation of solids on the bottom of the tank. The Madras Institute of Technology (MIT) at Anna University in Chennai, India, has a liquid conical tank controlled by a distributed control system (DCS) per the latest international standards for the process industry as shown in Figure 1. The use of a DCS in a university lab offers the opportunity for students to become proficient in industrial terminology, standards, interfaces and tools. The DCS allows graduate students and professors to explore the use of industry’s state-of-the-art advanced control tools. Less recognized is the opportunity to use the DCS for rapid prototyping and deployment of leading edge advances developed from university research.
The conical tank with gravity flow introduces a severe nonlinearity from the extreme changes in area. The dependence of discharge flow on the square root of the static head creates another nonlinearity and negative feedback. The process no longer has a true integrating response. In Appendix A online (www.controlglobal.com/1002_LevelAppA.html), the equations for the process time constant (τp) and process gain (Kp) are developed from a material balance applicable to liquids or solids. The equations are approximations because the head term (h) was not isolated. Since the radius (r) of the cross-sectional area at the surface is proportional to the height of the level as depicted in Figure 2, it is expected that the decrease in process time constant is much larger than the decrease in process gain with a decrease in level.
Controller Tuning Rules
The lambda controller tuning rules allow the user to provide a closed-loop time constant or arrest time from a lambda factor (λf) for self-regulating and integrating processes, respectively. The upper and lower controller gain limits are a simple fall out of the equations and can be readily enforced as part of the tuning rules in an adaptive controller.
For a self-regulating process the controller gain (Kc) and reset time (Ti) are computed as follows from the process gain (Kp), process time constant and process dead time (θp):
The upper gain limit to prevent fast oscillations occurs when the closed loop time constant equals to the dead time.
For an integrating process the controller gain (Kc) and reset time (Ti) are computed as follows from the integrating process gain (Ki) and process deadtime (θp):
The upper gain limit to prevent fast oscillations occurs when the closed loop arrest time equals the dead time:
The lower gain limit to prevent slow oscillations occurs when the product of the controller gain and reset time is too small.
Opportunities for Adaptive Control of Conical Tank Level
A linear PID controller with the ISA standard structure was tuned for tight level control at 50% level for a detailed dynamic simulation of the conical tank. Figure 3 shows that for setpoints ranging from 10% to 90%, a decrease in process time constant greater than the decrease in process gain at low levels causes excessive oscillations.
An adaptive controller integrated into the DCS was used to automatically identify the process dynamics (process model) for the setpoint changes seen in Figure 3. The adaptive controller employs an optimal search method with re-centering that finds the process dead time, process time constant, and process gain that best fits the observed response. The trigger for process identification can be a setpoint change or periodic perturbation automatically introduced into the controller output or any manual change in the controller output made by the operator.
Figure 4. Process models automatically identified for operating regions.
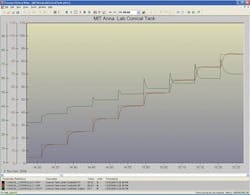
The process models are categorized into five regions as indicated in Figure 4. The controller gain and reset settings computed from the lambda tuning rules are then automatically used as the level moves from one region to another. This scheduling of the identified dynamics and calculated tuning settings eliminates the need for the adaptive controller to re-identify the process nonlinearity and tuning for different level setpoints. It was found that the use of lambda time, rather than lambda factors, with protection against going outside the controller gain limits helps provide a more consistent tuning criterion. As seen in Figure 5, the adaptive level controller eliminates the oscillations at low levels, and provides a more consistent level response across the whole level range.
Adaptive level controllers can eliminate tuning problems from the extreme changes in level control dynamics associated with different equipment designs and operating conditions. The integrated tuning rules prevent the user from getting into the confusing situations of upper and lower gain limits and the associated fast and slow oscillations. The smoother and more consistent response allows the user to optimize the speed of the level loop from fast manipulation of column reflux and reactor or crystallizer feed to slow manipulation of surge tank discharge flow control.
Greg McMillan is a consultant and ControlTalk columnist.
Sridhar Dasani is a graduate of Madras Institute of Technology (MIT) Anna University in Chennai India.
Dr. Prakash Jagadeesan is an assistant professor at Madras Institute of Technology (MIT) Anna University in Chennai India.

Leaders relevant to this article: