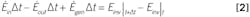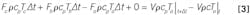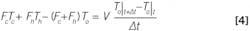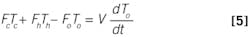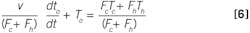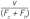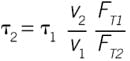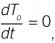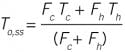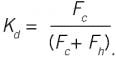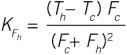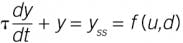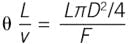Use first-principles techniques to get FOPDT coefficient values

Many control techniques are based on the ideal first-order plus dead-time (FOPDT) model of the process. Conventionally, we obtain model coefficient values by open-loop step-testing of the process; but this creates undesirable process upsets, and only reveals the local process behavior. This article suggests that simple phenomenological (first-principles mechanistic) modeling can provide coefficient values, without upsetting the process; and it also reveals how the values change with operating conditions.

Control techniques that use FOPDT models include PID tuning, gain scheduling, internal model control, and structuring feedforward and decouplers. In addition, appropriate pairing for single-input, single-output (SISO) loops in a multivariable control strategy, for instance using the relative gain array (RGA) technique, are based on the gains in FOPDT models. FOPDT descriptions also are commonly used to describe process dynamic responses. FOPDT modeling is important to control practice.

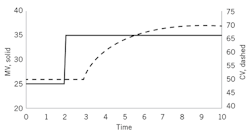
The FOPDT model coefficients relate to the process gain (response sensitivity to an input), the first-order lag time constant and the delay. Alternate names and acronyms include first-order lag plus delay (FOLPD). If there is a step-and-hold pattern in an input, the model pretends that the process responds with a first-order lag, after a delay. See Figure 1 for this ideal relation.

Often a Laplace notation is used to convey a FOPDT model:

Figure 1: Step-and-hold influence (manipulated variable, solid line) and ideal first-order process with dead-time response (controlled variable, dotted line).

μ̂ is the Laplace transformed influence variable, and γ̂ is the Laplace transformed response variable. K_p, τ_p and θ_p are the modeled idealizations for the process gain, time-constant and delay. A first-order model has one time-constant. It does not matter whether you prefer to show the values in a Laplace transfer function, list them in a table, show them in a differential equation, or simply describe them with text; the same three coefficients are in any FOPDT representation.

The objective is to obtain values for K_p, τ_p and θ_p.

Empirical approaches

The classic approach to determine coefficient values in FOPDT models is the reaction-curve method: Make a step-and-hold in the process influence from an initial steady-state value, observe the process response, wait until a final steady state, then use one of many techniques to fit a FOPDT model to the reaction curve. One of the original pre-computer techniques is to draw a line on the strip chart to extrapolate the point of most rapid controlled variable (CV) change to the initial and final values. Then read the delay and time-constant at the intersection points of the line and initial and final steady-state values. More recently, parametric methods are preferred, such as using the times for the CV to move ¼ and ¾ of the total CV change. Rather than this two-point fit, regression could be used to provide an overall best fit. All these methods return similar, but different, τ_p and θ_p values.

However, noise, disturbances and nonlinearity will often confound your ability to get a good model; and a one-sided step creates a deviation from a nominally desired CV value. To address these issues, make four steps in an up-down-down-up pattern. This provides four process responses. The average of the four responses will diminish the confounding characteristics, and the above and below aspects keep the process averaging about the nominal value. Even though the sequence of step-and-hold inputs tempers such effects, the τ_p and θ_p values still depend on the method to best fit the model to the data.

Unfortunately, the four-step sequence might take too long to be practicable. First, one must wait until an initial steady state, then wait for four subsequent steady states. Using a rough measure that steady state takes five time-constants, this means that the experimental period requires about 25 time-constants. If a time-constant is 10 minutes, this is an experimental duration of more than four hours, and it may not be possible to prevent external changes to operation or to permit such long periods away from setpoint, which may upset other human stakeholders. It also means that it requires frequent attention, and subjectivity to determine when the process is at each steady state within the vagaries of noise and uncontrolled disturbances.

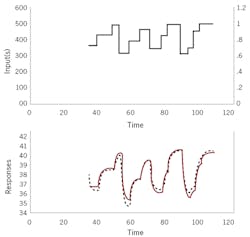
Figure 2: 'Skyline' influence on inputs (above) together with actual (solid, red) and model (black dotted) responses.

One method to accelerate the experimental process and to avoid the other undesirable aspects just mentioned is to use a skyline influence (so called because it resembles a city skyline) to replace the step-and-hold patterns, then best-fit the FOPDT model to the data in a least-squares regression. Figure 2 illustrates a skyline input, which is a series of random steps within a range, held for random durations up to about two time-constants. It also illustrates the response and a best fit model (see article, “FOPDT Modeling,” Control, Nov. ‘16). I also offer an Excel VBA program to generate the skyline pattern and best fit models to data on my website at www.r3eda.com.

Empirical problems

Empirical approaches get a locally valid model. However, if the process is nonlinear, the values for the gain, delay and time-constant will likely change with new operating conditions. Changes in external disturbances during the test will shift the response during the test. You can see from Figure 2 that the model approximately represents the data, but not exactly.

Further, as the process changes in time—perhaps due to tank levels changing, piping rerouting, raw material property changes or ambient influences—again, the values for the gain, delay and time-constant will likely change over time. Using empirical approaches to keep FOPDT models representative of the process as it continually changes may be onerous.

Things to accept

FOPDT models are not the process. Even if we term them as process models and use the subscript “p” on model coefficients, they are not. They're ideal approximations of reality. For example, if the process is high order without any delay, the FOPDT model (from a ¼ ¾ parametric fit) pretends that it has a first-order response after a pure delay. The ideal FOPDT model is not the process.

Empirical testing includes process nonlinearities, measurement noise, valve stiction and continuing unmeasured disturbances. Even if a process was truly FOPDT, getting coefficient values from empirical testing wouldn't return the true values.

The process behavior changes with operating level and due to continual changes in equipment, environmental influences and raw material. FOPDT models need to change over time.

The methods you use for getting the τ_p and θ_p values (one point, two point, or regression) return different values.

Although imperfect, FOPDT models are usually good enough for the control application. They provide a balance of sufficiency with perfection. Continuing that acceptable imperfection balance, use first-principles approaches to determine FOPDT model coefficient values.

First-principles approach

First-principles means to consider the major mechanisms. This contrasts with rigorous models, which seek to include even the minor mechanisms and perfectly model the constitutive relations. First-principles models are characteristic of what are used in college courses and introductory textbooks to explain heat exchangers, reactions, distillation, filters, etc.

To start, consider what accumulates (the inventory) that relates to the response of interest. For instance, a process doesn't inventory liquid level. Contents in a tank are added or removed, and the inventory is the volume of material. Level does not flow in or out, but it's a measure of that inventory. Similarly, a process doesn't inventory temperature. The inventory is thermal energy (heat) that's added or removed. Temperature is a measure of the heat that's accumulated. If you want to model a temperature response, consider mechanisms for heat addition or removal. If you want to model pressure response, consider mechanisms for adding or removing gas molecules.

The quantity being inventoried is often labeled as the conserved quantity. It doesn't disappear. Heat can be transferred, material can be transported or converted into reaction products, but neither disappear in chemical processes. Commonly, mass, momentum and energy are the conserved quantities.

Constitutive relations relate the quantity of inventory to the response. The ideal gas law, rearranged as P = nRT / V, could relate number of moles of gas (conserved quantity) in a volume at a particular temperature to the resulting pressure (response) that might be measured. A tank geometry could relate level to liquid volume, and liquid density could relate volume to mass. For a right circular cylinder, V = Πr²h and V = m/ρ, so the constitutive relation that relates level to the inventory of mass is V = m/(Πr²ρ).

Next, identify the point (or volume) in which the quantity being inventoried is accumulated. This could be a tank or vessel, volume of liquid in a heat exchanger tube, or a moving fluid.

Developing a first-principles dynamic model

I’ll use a simple example of mixing hot and cold fluid in a tank with a medium temperature outflow to illustrate the procedure.

Define a control volume: the tank contents.
Choose a conserved quantity: thermal energy because we're interested in the temperature response.
Assume: the water entering the tank is instantly and perfectly mixed. The contents are always spatially uniform.
Apply IOGA: this acronym refers to the inventory going In, less the inventory going Out, plus the inventory internally Generated, which is equal to the inventory Accumulated in a small increment of time, Δt.

Here, Ė_in represents rate of energy transferred or produced.

Insert the elementary constitutive relations between measurable variables and the IOGA quantities. i.e. Ė_out = F_oρc_pT_o, which assumes the reference temperature is 0 and the coefficients are constants.

There are two sources of heat inflow (both cold and hot water), one heat outflow (exit stream) and no internal reaction to generate heat. The thermal energy IOGA becomes:

Since ρ, c_p and V are considered constants, then F_out = F_c + F_h. Divide by ρc_p to simplify, and divide by Δt:

In the limit of very small ∆t, the finite difference is the derivative:

In standard ODE form:

Noteworthy regarding the time-constant:

as the units of time. It's a time-constant. It's the value of p needed for the FOPDT model.

Here, the time-constant is the volume for inventory accumulation divided by the flow rate through the volume. In general, τ_p is the capacity for the control volume to accumulate the relevant inventory divided by the rate through it.

If you know the value at one operating condition, then the equation shows how it scales with alternate operating conditions. It provides the gain scheduling rules:

Here the subscripts indicate two conditions, and the F_T represents total flow rate.

If you don’t trust your ability to get the models right, use the models to scale time-constants to other operating conditions.

Regarding the process order:

The one volume of inventory accumulation led to a first-order differential equation—a first-order response.
Two volumes of inventory, such as tanks in series, lead to two ODEs—a second-order response.

Regarding the gains:

At steady state,

so the equation shows that

is the steady state temperature (if F_c, T_c, F_h, or T_h all remain constant).

The first-principles model indicates what are the influence variables. On the righthand side, these are F_c, T_c, F_h and T_h.

If T_c is considered a disturbance, then the derivative of the steady-state temperature w.r.t. T_c is the gain of the disturbance. Here calculus is very easy:

If F_h is considered the controller influence, then the derivative of the steady state temperature w.r.t. F_h is the gain. Here calculus is not so easy:

If you're rusty on analytical calculus, use a finite difference numerical approach. Calculate T_o,ss for two similar F_h values, then calculate the gain by the ratio of the difference in T_o,ss values divided by the difference in the F_h values. The gain from the first-principles model is the gain needed in the FOPDT model.

The equation reveals how gain changes with operating conditions, which is a part of a gain scheduling rule.

If F_c, for instance is considered a wild flow, and F_h is to be controlled as a ratio, then the nominal ratio value is:

The actual value will likely need to be adjusted by feedback to compensate for sensor errors or influences not included in the model (such as ambient heat losses).

If, again, for instance, F_c and F_h are both being manipulated to manage two controlled variables, such as total flow rate and temperature, then gains from the steady-state equation can be used in a relative gain array procedure for loop pairing.

Your controller outputs are likely to be a % signal sent to a control valve, not individual F_c or Fh values. If you know the valve gain K_v, then the gain experienced by the controller is the K_{F_h}K_v product. (See article, “Understanding valve characteristics,“ Control, Aug. ’20).

If you don’t trust your ability to get the models right, trust your ability to use the models to scale gains to other operating conditions.

If you have the steady-state model y_ss = f(u,d), which you might from equipment design, process optimization or process analysis, then:

If there is one major volume of inventory, the model is first order, which means

With a modicum of process experience, you probably know a reasonable value for the process time-constant.

The steady-state model reveals the gains. Again, if you're rusty with calculus, use a finite difference approach.

Including a delay

Dead time is a delay from the event occurrence to its observation. Common examples are that thunder follows lightening by about five seconds per mile of distance. The batter hears the “crack” immediately, but the spectator, high in right field, hears it two seconds after seeing the batter swing.

The constitutive model for transport delay in a pipeline is:

(if ideal plug flow). In the mixing tank example, if the mixed fluid temperature is measured downstream of the tank, then there would be a transport delay. There might also be delays due to sample transport to either the lab or the online analytical instrument, and then there's the lab analysis time or online analytical instrument cycle time. If there is a dominant lag, but there are several smaller lags, the time-constants for the smaller lags can be considered as pseudo delays. For example, if the thermowell and the control valve have three-second and one-second time-constants (which are small compared to a one minute time-constant for the tank), these can be modeled as delays. Add all the delays to get the total:θ_total = θ₁ + θ₂ + θ₃ + .... This θ_total is the value needed in the FOPDT model.

Typically, delays from sampling interval or communication devices are inconsequential.

Noteworthy regarding delays:

The model indicates how delay scales with operating conditions. For instance, if only flow transport:

Even if a bit more complicated, the models can be used for gain scheduling rules.

If you don’t trust your ability to get the models right, trust your ability to use the models to scale delays to other operating conditions.

Key takeaways

Even though the FOPDT reaction-curve concept is presented as a response to a step-and-hold influence, if you're seeking to get process data to generate model coefficient values, use a skyline input pattern to generate empirical data.

However, consider using first-principles model approaches. First-principles models can:

Provide values for FOPDT model coefficients, saving considerable time and money, and avoiding process upsets.
Provide insight for control structure, such as which variables should be considered as manipulated variables and which are disturbances, assigning loop pairing, and whether to choose a ratio or feedforward strategy.
Reinforce a mechanistic process understanding, which has many benefits in troubleshooting and process improvement.
Reveal the FOPDT model coefficient values. Don’t use calculus derivatives to get the gains. Use a numerical, finite-difference approximation. And certainly, even though the model may be a differential equation, don’t solve dynamic models. Use the information to solve a process problem.
Generate adequate FOPDT coefficient values. FOPDT idealization is not the process. Even with the best FOPDT model, the process is not FOPDT. Further, the coefficients are corrupted by noise and disturbances and the method to determine p and p values. Classic modeling approaches are imperfect, as are first-principles approaches. As long as the FOPDT coefficient values are reasonable, the model will be useful.

About the author: R. Russell Rhinehart

Russ Rhinehart started his career in the process industry. After 13 years and rising to engineering supervision, he transitioned to a 31-year academic career. Now “retired," he returns to coaching professionals through books, articles, short courses, and postings to his website at www.r3eda.com. He can be reached at [email protected].