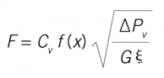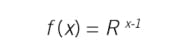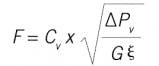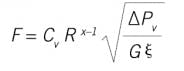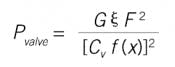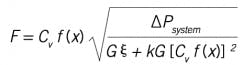The valve characteristic represents how the flow rate through a valve changes with valve position. Desirably, for normal use, we want the characteristic to be linear (Figure 1), a constant gain, so that controller tuning at one flow rate is acceptable for all flow rates.
The idealized valve equation is:
Where F is the volumetric flow rate (gal/min, L/s, SCFM/hr, etc.) and Cv is the valve capacity, the flow rate(same units as F) at full open conditions. ΔPv is the pressure drop across the valve that's pushing the fluid through it (psi, Pa, etc.), G is the fluid specific gravity, and ξ has a value of 1 with the same units as ΔPv to make the equation dimensionally correct. Usually, ξ is not shown, since its value is unity. Finally, f(x) is the valve characteristic, the fraction of maximum flow as a function of valve stem position, x. Both f(x) and x are dimensionless, and they range from zero to 1. When the stem is closed, x = 0, the fraction of maximum flow is also zero, f(x) = 0. And when the stem is fully open, x = 1, the fraction of maximum flow is also unity, f(x) = 1.
Figures 1 and 2: A linear flow rate response (left) and three categories of valve characteristics (right).
Three types of valve characteristics
Figure 2 illustrates three valve characteristics.
The linear characteristic is the middle line, where f(x) = x. The upper curve is called a quick opening characteristic, meaning that small initial openings of the stem permit a very large flow-through. This might be good where emergency flooding/dousing is important. The lower curve represents a modified equal percentage characteristic. Even up to 50% open, the valve is just up to 20% capacity. The ideal equal percent relation has an equal fractional flow increase, ΔF⁄F, for each incremental stem change, Δx. After a bit of math the relation is:
R is termed rangeability. Unfortunately, when the stem is closed, x = 0, the fraction of maximum flow is not zero, f(x) = 1/R. So, an equal percent valve is modified at low stem positions to shut off when x = 0.
Why have such a valve? Consider a linear valve characteristic, f(x) = x, the middle line in Figure 2. Note that the valve model of Equation (1) indicates that the flow rate through the valve depends on the pressure drop across the valve. For a linear characteristic, the valve equation is:
Whether the ∆Pv is high, medium or low, the flow rate is linearly related to the stem position as indicated in Figure 3 by the solid lines for a high, medium and low ∆Pv.
The issue is that when a valve is installed in a line, the ∆Pv doesn't remain constant. The pressure drop across the valve changes as the valve changes the flow rate. When the valve is closed, the valve blocks the flow, and it must hold back the entire driving pressure that wants to make the fluid flow, perhaps a combination of pump, gravity and up- and downstream pressures, ∆Psystem. In this fully closed, x = 0 case, the pressure drop across the valve is high, ∆Pv = ∆Psystem. At an intermediate stem position, perhaps 50%, the flow rate through the piping system is medium, and the pressure drop due to friction losses in the piping system, ∆Ppipe, is also medium. This means the pressure drop across the valve is medium:
By contrast, when the valve is fully open and the flow rate is large, the friction loss pressure drop through the piping system is high, leaving a low ∆Pv. The large dots on the linear relations in Figure 3 represent which ∆Pv is associated with the valve stem position. The dashed line is the locus of how the flow rate trends with valve position. Even though the isolated (inherent when ∆Pv is kept constant) valve characteristic is linear, the linear valve has a quick-opening nature when installed because ∆Pv depends on the flow rate, which depends on x. This means a controller tuned for the higher flow rates (low process gain, small changes in flow rate for a given change in controller output) will be too aggressive for the low-flow (high process gain) conditions. As illustrated in Figure 3, the process gain (flow rate response to controller output) has about an 18:1 ratio.
Figure 3 and 4: The installed characteristic of a linear valve (left) and an equal-percent valve (right).
The installed characteristic (flow rate response to valve stem position) is not the same as the inherent characteristic (where some magic might keep ∆Pv a constant).
The same process flow attributes affect an equal percentage (=%) valve. Here, the ideal valve model is:
Flow rate depends on pressure drop, too
In Figure 4, the solid lines again are the plots of flow rate through an = % valve when ∆Pv is a constant at high, medium and low values. The dashed line is the installed characteristic. Notice now for the installed characteristic the process gain is nearly the same at all flow regions. With the = % valve, the gain ratio is reduced from 18 to about 3.
These illustrations represent an ideal model for pressure losses in the piping system and valve characteristics with an = % rangeability of 40. Valve manufacturers don’t have to use Equation (2) for a valve model, and they may offer products with alternate Cv and R values, so get details from your valve vendor. Although ideally represented here, the concepts are the same for real valves installed in real flow systems.
You can explore the impact of Cv and R values for a flow control valve (FCV) in your particular piping system. Ideally, if the system pressure drop driving flow, ∆Psystem, is a constant and the friction losses through the piping system are modeled as being proportional to the square of the flow rate, ∆Ppiping losses = k G F2 and the valve model is inverted to determine the ∆Pvalve :
And the installed valve characteristic can be modeled by substituting relations in the pressure balance, ∆Psystem = ∆Ppipe + ∆Pvalve and solving for flow rate. The installed flow rate model is:
Use f(x) = x for a linear valve and f(x) = Rx-1 for an ideal = % valve. Adjust the value of Cv to get your desired, fully-open flow rate, and R to get a close-enough-to-linear installed characteristic. Of course, if you want to include non-idealities like how the outlet pressure of a centrifugal pump changes with flow rate, you can.
There are many aspects of FCV selection. Hopefully, this article will help you understand one of them. I think technical bulletins and monographs from valve manufacturers provide excellent and comprehensive tutorials.
About the Author
R. Russell Rhinehart
Columnist
Russ Rhinehart started his career in the process industry. After 13 years and rising to engineering supervision, he transitioned to a 31-year academic career. Now “retired," he returns to coaching professionals through books, articles, short courses, and postings to his website at www.r3eda.com.

Leaders relevant to this article: