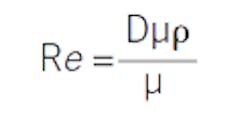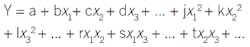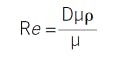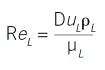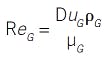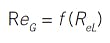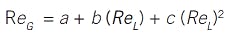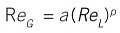How insight, math can simplify modeling and optimize experiment design
Often, we desire a mathematical model of a process or product. For example, I've needed to know: How does waste generation depend on the processing properties and controller coefficient values during a product changeover? How does column flooding depend on fluid properties and operating conditions? How does a particle filter performance depend on its structure properties?
Once we have an adequate model, it can guide our choices to improve design and operation. It may be possible to obtain a phenomenological model, but in each of the cases mentioned above, the complexity of the mechanisms and associated equations have been beyond my reach. When this happens, we need to generate empirical models—models from data. There are many approaches. I recommend you consider using dimensionless group models.
For this article, I’ll use flooding in a packed column absorber as an example. This is not an article about unit operation. It’s about dimensionless group models, a practicable and effective approach to modeling complex phenomena. However, a brief description of the process and modeling objective is necessary.
Gas absorption
In a gas absorption column, gas travels upward through a packed column. The packing is generally open, but it creates a tortuous path splitting and recombining the upward flowing gas. Liquid enters the top of the column, falls by gravity, and splashes downward, coating, then dripping off of the packing and splashing on the packing below. The column is not filled with liquid. Most of the space within the column is upward flowing gas. The liquid is raining and splashing as it falls downward through the packing matrix. The objective of the packing is to create liquid-gas surface area, so the liquid can absorb a component in the gas. The liquid cleans the gas.
Such absorption unit operations (and their converse, stripping) are common in the chemical and fuel processing industries, and flooding is an operating issue in the unit.
In flooding, sections of the column undesirably fill with liquid. Here’s why: if the gas is flowing upward too fast, then small liquid droplets that should be falling are blown upward, and extra liquid accumulates on the packing above. Eventually, the lift of droplets in the gas makes the gravity rate-of-fall of the liquid within the column less than the flow rate entering the column. Then the column fills up with liquid, and the gas becomes bubbles rising within the liquid. This flooding has many undesirable aspects.
This modeling exercise is to determine a mathematical relation between liquid and gas properties to indicate the non-flooding, safe operating region. Data will be generated on a pilot-scale unit by selecting gas, liquid and operating conditions, progressively stepping up the gas flow rate (G), and observing the pressure drop (dP) of the gas through the column. At each step increase of G, this dP increase is larger, but at flooding, dP does not asymptotically approach a steady value—it accelerates in an open-loop, unstable manner. When this is observed, flooding will be declared.
Developing a model
Start by asking the generic question, “What influences might affect the outcome?” For the column flooding, it is “What conditions might affect flooding, and thereby define a limit on the gas flow rate, G?” Here are some: Liquid flow rate, L, and the liquid properties of density, ρL, and viscosity, µL; column diameter (or some other characteristic dimension that restricts the flow paths); and gas properties of density, ρG, and viscosity, σG. Since the column properties (length, diameter, packing type) will not be changed, we're left with G = f(L, ρL, µL, d, ρG, σG ). In general, this can be expressed as a response variable y, which is a function of the six influences, x1, x2, …, x6. Of course, you might be considering the model of another case, in which there could be a larger or smaller number of influences.
A classic statistical approach to developing empirical models is to express the cause-and-effect relation as a polynomial model. Justification for this is grounded in a Taylor Series expansion of any function. If a quadratic model has adequate functional relations, then the model has this form:
The first coefficient, a, is the intercept. Coefficients b, c, d, and so on, represent the linear terms. Coefficients j, k, l, and so on, represent the homogeneous quadratic terms; and r, s, t, and so on represent the cross-product terms. In this quadratic model, with the six influence variables, there are 28 coefficients. A rule of thumb in empirical modeling is that there should be three independent experiments for each coefficient, so here, about 84 independent experiments. That's a lot. And still, the quadratic functionality may not be adequate—more terms may be needed. Further, considering how to independently adjust viscosity and density, perhaps by operating pressure and temperature, suggests some very expensive experimentation.
Here is where dimensionless group models save the day. You're probably familiar with many dimensionless groups. The Mach number is the ratio of speed in air to the speed of sound. The Reynolds number is the ratio of momentum advection to diffusion, which is the determining factor as to whether flow is turbulent or laminar. Dimensionless groups are ratios and products of constituent variables in which the units cancel. For example, the Reynolds number is a characteristic length times velocity times density divided by viscosity:
Using the classic “English” units of feet, feet per second, pounds mass per cubic foot, and pounds mass per foot-second, it is easy to see that the units cancel, and that Re is dimensionless. Regardless of the system of units you might choose, Re is dimensionless and retains its same numerical value.
In this particular example, the six variables are combined into two dimensionless groups. (To see how, look for instruction on the Buckingham Pi method, although intuitive arrangements are often fully adequate.) One is the Reynolds number for the liquid:
and the other for the gas:
Mathematical analysis indicates that the model can be expressed as just the two variables:
Here, the independent aspects of density, diameter and viscosity are combined, and it doesn’t matter what the constitutive variable values are; it's the combined impact that's relevant, and the dimensionless groups define that relation.
Now, if a quadratic relation was acceptable, one might use:
This is a great reduction in the number of model coefficients, work in generating coefficient values, and experimental costs to generate the data. However, the relation might not be well described with a quadratic, and experience has shown that a power law model is often better:
This power law model is more flexible, and only has two coefficients. Using the heuristic of three independent experiments per coefficient, only six experiments are now desired. Further, the individual values of viscosity and density are not important. Since the value of the dimensionless group is what is important, it doesn't matter what variable is used to change the ReL value to generate experimental data; what matters is the ReL value. So, although there must be an assessment of viscosity and density to calculate ReG and ReL, the experimental design can be fully defined by simply changing the liquid and gas flow rates, again providing a great convenience.
Figure 1: Reynolds number (Re) data from a pilot-scale packed tower absorber (circles) define a model (solid line) with 95-percentile limits indicated by dashed lines. Source: Trey Holloway, Jeffrey Kibler and Zach Spiegel.
Data and model
The open circles in Figure 1 reveal data from the pilot-scale packed tower absorber from our undergraduate chemical engineering lab at Oklahoma State University. The column is about 8 in. in diameter with about 12 ft. of packed length over two sections. The data are from air-water trials generated by Trey Holloway, Jeffrey Kibler and Zach Spiegel in the spring of 2014, and appreciatively used with their permission.
The solid curve represents the model. Since there is uncertainty in both the independent and dependent variables, coefficients were adjusted to minimize the squared normal residual (this is variously termed total SSD or perpendicular SSD), not the conventional vertical SSD. I used Akaho’s method to approximate the normal SSD as an idealization of a maximum likelihood method. It accounts for variability in both the x and y variables.
The model is the solid line, and the 95-percentile limits of the model due to variability in the data (calculated by a technique called bootstrapping) are indicated by the dashed lines.
If you're seeking more information (including model validation, experimental design, total least squares, and bootstrapping to determine the confidence limits of a regression model), refer to my book: Nonlinear Regression Modeling for Engineering Applications, John Wiley & Sons, 2016, ISBN 9781118597965. Directions on the Buckingham Pi method to develop dimensionless groups are easily accessed in Internet searches. A great starting place is here.
[pullquote]
The pilot-scale modeling invites a number of observations:
- The data reveals a hyperbolic sort of relation. The value of coefficient p in the model is -0.869, which is definitely neither linear nor quadratic, which indicates the simplicity of the power law structure in finding the right functionality over the classic power series representation.
- Although the experimentation led to selecting ReL as the independent variable and ReG as the dependent variable, the reverse choice would have been as easily made. In some years, the students set the water flow rate and increase the air flow rate to the flooding point. The user choice does not specify a cause-and-effect mechanism.
- The fundamental nature of dimensionless groups in modeling can be revealed in several ways. Here, students used the Buckingham Pi method. Classically, scaling of a differential equation to make each term non-dimensional reveals the groups, which also reveals that the coefficients to the equation (hence its solution) are not fundamentally the individual primitive variables, but are the ratios and products that create the dimensionless groups.
- The utility of dimensionless analysis is evidenced in the design scale-up and model scale-down classic in fluid dynamics and design of ship hulls, furnaces, airplanes and automobiles. The reader should also be familiar with charts that use dimensionless variables to unify similar trends to a common graph. These include fluid drag factor response to Reynolds numbers, and cooling rate response to Fourier number. And, many of our fundamental design models are developed with dimensionless groups: Consider the Dittus-Boelter relation.
- Often, conversion factors need to be included to make terms dimensionless. These include the often missing gc in F = ma and the various Bernoulli relations, the conversion equivalents of mechanical to thermal energy, or of centipoise to system units of the other variables.
- This method doesn't mean that you've included all of the relevant variables, and excluded irrelevant variables. Intuitive guidance and progressive insight as you develop the models is important. The results of the first modeling attempt will reveal aspects that shape the second attempt. But, of course, this is true for any approach to modeling, whether it be phenomenological, classic empirical or big-data.
- Any dimensionless number can be expressed in any number of ways, for instance, multiplying and dividing the classic Re expression by cross sectional area, A = πD2 / 4, and combining Aup to represent mass flow rate, M, results in Re = (πM) / 4Dμ. Note that π is dimensionless, and Re can be expressed as the product of two dimensionless groups, Re = (π)(M / 4Dμ). And any dimensionless number can be inverted and redefined as “my” number, My = 4Dμ / M. You might devise such a number, which might not be easily recognized as the reciprocal of the classic Reynolds number. My experience indicates that initially devised dimensionless groups can usually be rearranged to classic dimensionless groups: Reynolds, Nusselt, Froude, Galileo, Fourier, Eckert, Peclet, Sherwood, etc.
- The column internals (packing supports, flow redistributors and such) will have a significant impact on the flooding curve, making the data-regressed model a unit-specific model.
- The power law relation is not derived from fundamentals. It has been found to provide adequate models from diverse applications. It is a useful tool. Sometimes extrapolation of the model to very large or small values provides insight about alternate model forms or segregated regions of validity.
About the Author
R. Russell Rhinehart
Columnist
Russ Rhinehart started his career in the process industry. After 13 years and rising to engineering supervision, he transitioned to a 31-year academic career. Now “retired," he returns to coaching professionals through books, articles, short courses, and postings to his website at www.r3eda.com.

Leaders relevant to this article: