Sustainability: Orifice Rangeability; Non-Renewable Energy Sources

"Ask the Experts" is moderated by Béla Lipták (http://belaliptakpe.com/), process control consultant and editor of the Instrument Engineer's Handbook (IEH). The 5th edition is in the planning stages. If you would like to contribute by updating an existing or preparing a new chapter, or if you have questions for our team of experts, please write to [email protected].

Q: If I use a square root extractor and a digital transmitter with very high accuracy, such as .065%, is it possible to measure flows of less than 30%, or is the rangeability governed by the orifice characteristics?

Adi Varaghan
[email protected]

A: The flow error = the D/P error/2F where F is the fractional flow (0-1.0). With a D/P error of 0.065%, your flow error would be 1% at F = 0.032 or 3.2%. (This does not include any error in the orifice plate.)

The rangeability of orifice meters can be extended by using 2-D/P transmitters. For example, a range of 0-100"WC can be used for full-range flow, and a range of 0-11.11"WC for 0% to 30% of full-range flow. This gives a rangeability of 30:1 in flow. Switching between the two transmitters must take place at 30% flow.

Greg Shinskey
[email protected]

A: ISO standards are used for the design and installation of an orifice device. The deviation from the square root model is visually detectable. (Rhinehart, et al., "A Power Law Approach to Orifice Flow Rate Calibration," ISA Transactions, Vol. 50, No. 2, 2011, pp. 329-341). Many orifice flowmeters are not ISO-compliant. If the discharge coefficient is calculated from equations, such as the Reader-Harris or Stolz, then the discharge coefficient value has an error of about 0.7%. Since the square-root model is used to convert the measured D/P to a calculated flow rate, this combination limits accuracy to about 1% for the upper 5:1 range for ISO-compliant devices, and asymptotically rises for the lower flow rate conditions. For non-compliant devices, the deviation from the ideal square-root relation is larger. Further, the calibration of the D/P transducer and other signal conversion devices is critical. Regardless of the discrimination error (truncation error, digital device precision) of elements in the signal processing path, the calculations that report the flow rate are still based on the square-root model, coefficient values, device calibration and turbulent-induced noise. The impact of these influences cannot be reduced with smaller discrimination error in a digital device.

R. Russell Rhinehart
[email protected]

The reversible fuel cell (RFC)

Figure 1: In some respects, the development of the RFC is more of a challenge than was that of the PC, because it also requires the development of new catalysts and total automation to the point where its use will be as simple as that of a thermostat.A: You may measure the D/P (though the orifice coefficient is a function of Reynolds number), but you will find an analog square root extractor fails to follow the theoretical curve below about 25% flow (6% of full scale D/P measurement). Check out the Emerson handbook on square root extraction in D/P transmitters. They use a bi-linear fit at the bottom end to enable calibration adjustment.

Ian H. Gibson
[email protected]

A: I recently reviewed an article that indicated that Emerson makes such a transmitter: the Rosemount 3051S Ultra for Flow.

Ian Verhappen
[email protected]

A: There is no point in spending a great deal of time and money on obtaining higher orifice rangeabilty unless that effort is justified. The modern D/P cell is far better than the old ones, and the old 3:1 flow range rule of thumb can be stretched. Best is a calibrated orifice run. It is important to determine what the Reynolds number is over the intended range and how it will affect the orifice coefficient. Very wide ranges are possible with automatic switching of alternate orifice runs and with multiple transmitters with different calibrations. If the process engineers can't accurately determine the fluid properties then the meter can't be any more accurate than the information provided.

Cullen Langford
[email protected]

Q: In your book, Post-Oil Energy Technology, you published your best estimate of the total amounts of exhaustible energy deposits and the rates at which we are using them. Since then, new deposits have been found, and other changes have taken place. Can you sum up your view today?

H. Crowney
[email protected]

A: I will use ZJ (zetajoule = 1021 BTU) units in giving you my best estimates. Before doing that I will give you a sense of how much a ZJ is

10 million supertankers of oil;
300 TWh (1012 KWh) of electricity;
The production of 12,000 nuclear power plants;
400 million railroad cars of coal;
30 trillion m3 of natural gas.

The data in Table 1 is from a lecture I gave on the AT&T Tech Channel last month. The numbers given are for the year 2011. The RTU (reserve-to-use ratio) does not mean that the deposits will last for that many years, partly because during the last century the global energy consumption has increased by more than tenfold, and partly because the rate of demand increase has already exceeded the rate of new discoveries. The data for nuclear energy is based only on fission reactors and does not consider breeder or fusion designs because they are orders of magnitude more dangerous.

According to my calculations, if 1% to 2% of the global GDP were invested in the conversion to renewable energy, the total conversion could be completed by the end of this century. This sum is less than what is spent on energy wars today or on "scraping the bottom of the energy barrel," while risking environmental and nuclear disasters.

I might also note that in the process of converting to a clean and inexhaustible lifestyle, mankind will not only experience the third industrial revolution (the second was the information revolution that we experience today), but will find that implementing the new technologies will create more jobs than did the Marshall Plan.

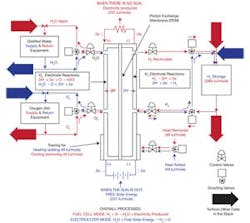
Just consider the development and production of the RFC (my reversible fuel cell shown in Figure 1), the controls of which I will describe in my keynote address at the ISA Show and Conference in October. If interested, you can read about it at http://belaliptakpe.com/solar-hydrogen-power-plant/the-reversible-fuel-cell-rfc/.

Béla Lipták
[email protected]